
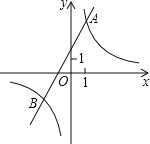
【题目】如图,已知反比例函数y1=![]() 的图象与一次函数:y2=ax+b的图象相交于点A(1,4)、B(m,﹣2)
的图象与一次函数:y2=ax+b的图象相交于点A(1,4)、B(m,﹣2)
(1)求出反比例函数和一次函数的关系式;
(2)观察图象,直按写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C是x轴上的点,且△ABC的面积面积为6,求点C的坐标.
【答案】(1)反比例函数的解析式为y1=![]() ,一次函数的解析式为 y2=2x+2;(2)﹣2<x<0或x>1;(3)C的坐标(1,0)或(﹣3,0).
,一次函数的解析式为 y2=2x+2;(2)﹣2<x<0或x>1;(3)C的坐标(1,0)或(﹣3,0).
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据一次函数图象在上方的部分是不等式的解,可得答案;
(3)根据面积的和差,可得答案.
(1)∵函数y1=![]() 的图象过点A(1,4),即4=
的图象过点A(1,4),即4=![]() ,
,
∴k=4,即y1=![]() ,
,
又∵点B(m,﹣2)在y1=![]() 上,
上,
∴m=﹣2,
∴B(﹣2,﹣2),
又∵一次函数y2=ax+b过A、B两点,
即 ![]() ,
,
解之得![]() .
.
∴y2=2x+2.
反比例函数的解析式为y1=![]() ,
,
一次函数的解析式为 y2=2x+2;
(2)要使y1<y2,即函数y1的图象总在函数y2的图象下方,
∴﹣2<x<0或x>1;
(3)如图,直线AB与x轴交点E的坐标(﹣1,0),
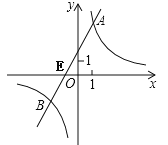
∴S△ABC=S△AEC+S△BEC=![]() EC×4+
EC×4+![]() EC×2=6.
EC×2=6.
∴EC=2,
-1+2=1,-1-2=-3,
∴C的坐标(1,0)或(﹣3,0).


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】春节即将来临时,某商人抓住商机购进甲、乙、丙三种糖果,已知销售甲糖果的利润率为![]() ,乙糖果的利润率为
,乙糖果的利润率为![]() ,丙糖果的利润率为
,丙糖果的利润率为![]() ,当售出的甲、乙、丙糖果重量之比为
,当售出的甲、乙、丙糖果重量之比为![]() 时,商人得到的总利润率为
时,商人得到的总利润率为![]() ;当售出的甲、乙、丙糖果重量之比为
;当售出的甲、乙、丙糖果重量之比为![]() 时,商人得到的总利率为
时,商人得到的总利率为![]() .那么当售出的甲、乙、丙糖果重量之比为
.那么当售出的甲、乙、丙糖果重量之比为![]() 时,这个商人得到的总利润率为______.
时,这个商人得到的总利润率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,a、c满足![]() .AB表示点A、B之间的距离,且
.AB表示点A、B之间的距离,且![]() .
.
![]()
(1)![]() ________,
________,![]() ________;
________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数________表示的点重合;
(3)点A、B、C在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则![]() ________,
________,![]() ________.(用含t的代数式表示)
________.(用含t的代数式表示)
(4)在(3)的条件下,请问:![]() 的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
1×2=![]() (1×2×3﹣0×1×2)
(1×2×3﹣0×1×2)
2×3=![]() (2×3×4﹣1×2×3)
(2×3×4﹣1×2×3)
3×4=![]() (3×4×5﹣2×3×4)
(3×4×5﹣2×3×4)
由以上三个等式相加,可得:1×2+2×3+3×4=![]() ×3×4×5=20,读完以上材料,请你计算下列各题:
×3×4×5=20,读完以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(写出过程)
(2)1×2+2×3+3×4+…+n×(n+1)= ;
(3)1×2×3+2×3×4+3×4×5+…+9×10×11= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用12 m长的一根铁丝围成长方形.
(1)如果长方形的面积为5![]() .那么此时长方形的长是多少?宽是多少?如果面积是8
.那么此时长方形的长是多少?宽是多少?如果面积是8![]() 呢?
呢?
(2)能否围成面积是10![]() 的长方形?为什么?
的长方形?为什么?
(3)能围成的长方形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
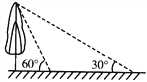
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l为x+y=8,点P(x,y)在l上且x>0,y>0,点A的坐标为(6,0).
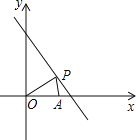
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图形面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
(1)根据下列所示图形写出一个代数恒等式 .
(2)已知正数a,b,c和m,n,l,满足ambnclk,试构造边长为k的正方形,利用图形面积来说明albmcnk2.
思考过程如下:
因为ambnclk,所以a,b,c,m,n,l,均 k(填“大于”或“小于”).由于k2可以看成一个正方形的面积,则al、bm、cn可以分别看成三个长方形的面积.请画出图形,并利用图形面积来说明albmcnk2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com