
【题目】1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即:![]() 如果正整数
如果正整数![]() 最少经过6步运算可得到1,则
最少经过6步运算可得到1,则![]() 的值为__________.
的值为__________.
科目:初中数学 来源: 题型:
【题目】已知,数轴上点![]() 在原点左边,到原点的距离为8个单位长度,点
在原点左边,到原点的距离为8个单位长度,点![]() 在原点的右边,从点
在原点的右边,从点![]() 走到点
走到点![]() ,要经过32个单位长度.
,要经过32个单位长度.
(1)求![]() 、
、![]() 两点所对应的数;
两点所对应的数;
(2)若点![]() 也是数轴上的点,点
也是数轴上的点,点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到原点的距离的3倍,求点
到原点的距离的3倍,求点![]() 对应的数;
对应的数;
(3)已知,点![]() 从点
从点![]() 向右出发,速度为每秒1个单位长度,同时点
向右出发,速度为每秒1个单位长度,同时点![]() 从点
从点![]() 向右出发,速度为每秒2个单位长度,若点
向右出发,速度为每秒2个单位长度,若点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到原点
到原点![]() 距离相等,则点
距离相等,则点![]() 到原点
到原点![]() 距离与点
距离与点![]() 到点
到点![]() 的距离与值是否变化?若不变,求其值.
的距离与值是否变化?若不变,求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
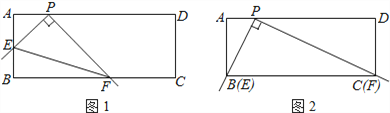
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠ PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
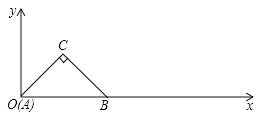
【题目】(3分)在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽销售渠道,某水果商店计划将146个柚子和400个橙子装入大、小两种礼箱进行出售,其中每件小礼箱装2个柚子和4个橙子;每件大礼箱装3个柚子和9个橙子.要求每件礼箱都装满,柚子恰好全部装完,橙子有剩余,设小礼箱的数量为x件.
(1)大礼箱的数量为________件(用含x的代数式表示).
(2)若橙子剩余12个,则需要大、小两种礼箱共多少件?
(3)由于橙子有剩余,则小礼箱至少需要________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践动手操作:用矩形下的折叠会出现等腰三角形,快速求BF的长.
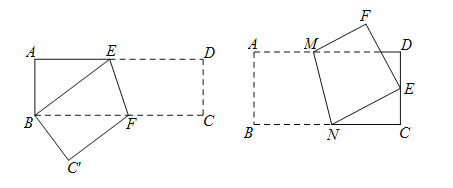
(1)如图,在矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点D与点B重合,折痕为EF,则等腰三角形是 ;
(2)利用勾股定理建立方程,求出BF的长是多少?
(3)拓展:将此矩形折叠,使点B与DC的中点E重合,请你利用添加辅助线的方法,求AM的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
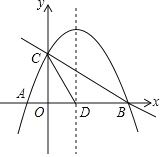
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交于点
、B两点,与y轴交于点![]() ,抛物线的对称轴交x轴于点D.
,抛物线的对称轴交x轴于点D.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的值;
的值;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 六个点,点
六个点,点![]() 在原点位置,点
在原点位置,点![]() 表示的数为
表示的数为![]() ,已知下表中
,已知下表中![]() 的含义均为前一个点所表示的数与后一个点所表示的数的差,比如
的含义均为前一个点所表示的数与后一个点所表示的数的差,比如![]() 为
为![]() .
.
|
|
|
|
|
|
|
|
|
|
若点![]() 与点
与点![]() 的距离为
的距离为![]() ,则
,则![]() 的值为________
的值为________
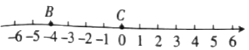
查看答案和解析>>
科目:初中数学 来源: 题型:
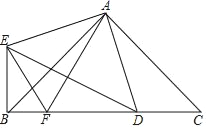
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com