
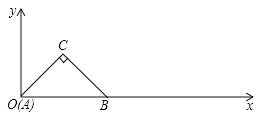
【题目】(3分)在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为 .
科目:初中数学 来源: 题型:
【题目】在桌面上,有若千个完全相同的小正方体堆成的一个几何体![]() ,每个小正方体的边长为
,每个小正方体的边长为![]() ,如图所示.
,如图所示.
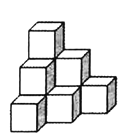
![]() 请画出这个几何体
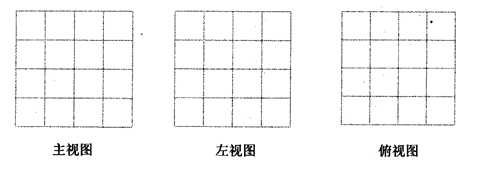
请画出这个几何体![]() 的三视图. (用黑色水笔描清楚);
的三视图. (用黑色水笔描清楚);
![]() 若将此几何体
若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则几何体
的表面喷上红漆(放在桌面上的一面不喷),则几何体![]() 上喷上红漆的面积为
上喷上红漆的面积为 ![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
![]() 若现在你的手头还有这样的一些边长为
若现在你的手头还有这样的一些边长为![]() 的小正方体可添放在几何体
的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
上,要保持主视图和左视图不变,则最多可以添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ABCD 中,对角线 AC、BD 相交于点 O,过点 D 作对角线 BD 的垂线交 BA 的延长线于点 E.
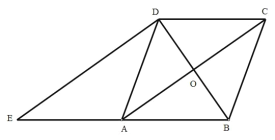
(1)证明:四边形 ACDE 是平行四边形;(2)若 AC=24,BD=18,求△ADE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店以每件80元的进价购进某种商品,原来按每件100元的售价出售,一天可售出50件;后经市场调查,发现这种商品每件的售价每降低2元,其销售量可增加10件.
(1)该网店销售该商品原来一天可获利润 元.
(2)设后来该商品每件售价降价![]() 元,网店一天可获利润
元,网店一天可获利润![]() 元.
元.
①若此网店为了尽可能增加该商品的销售量,且一天仍能获利1080元,则每件商品的售价应降价多少元?
②求![]() 与
与![]() 之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即:![]() 如果正整数
如果正整数![]() 最少经过6步运算可得到1,则
最少经过6步运算可得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外学习时间情况,随机抽取部分学生进行问卷调查,并将调查结果分为 A,B,C,D 四个等级.设学习时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2 ,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
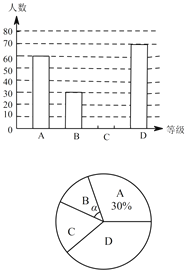
(1)该校共调查了多少名学生;
(2)将条形统计图补充完整;
(3)求出表示 B等级的扇形圆心角 α 的度数;
(4)在此次问卷调查中,甲班有 2 人平均每天课外学习时间超过 2 小时,乙班有 3 人平均每天课外学习时间超过 2 小时,若从这 5 人中任选 2人去参加座谈,试用列表或画树状图的方法求选出的2人
来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一渔船在A处与小岛C相距70海里,若该渔船由西向东航行30海里到达B处,此时测得小岛C位于B的北偏东30°方向上,则该渔船此时与小岛C之间的距离是_____海里.
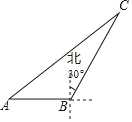
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com