
【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度是多少?

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。

查看答案和解析>>
科目:初中数学 来源: 题型:
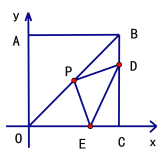
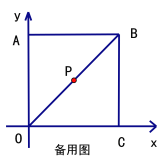
【题目】在直角坐标系中,正方形OABC的边长为8,连结OB,P为OB的中点.
(1)直接写出点B的坐标B( , )
(2)点D从B点出发,以每秒1个单位长度的速度在线段BC上向终点C运动,连结PD,作PD⊥PE,交OC于点E,连结DE.设点D的运动时间为![]() 秒.
秒.
①点D在运动过程中,∠PED的大小是否发生变化?如果变化,请说明理由如果不变,求出∠PED的度数
②连结PC,当PC将△PDE分成的两部分面积之比为1:2时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
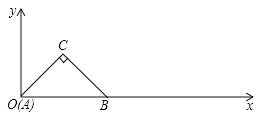
【题目】(3分)在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践动手操作:用矩形下的折叠会出现等腰三角形,快速求BF的长.
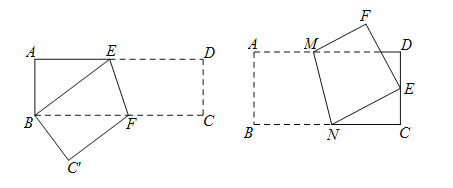
(1)如图,在矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点D与点B重合,折痕为EF,则等腰三角形是 ;
(2)利用勾股定理建立方程,求出BF的长是多少?
(3)拓展:将此矩形折叠,使点B与DC的中点E重合,请你利用添加辅助线的方法,求AM的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
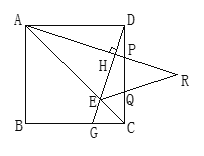
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com