
【题目】综合与实践动手操作:用矩形下的折叠会出现等腰三角形,快速求BF的长.
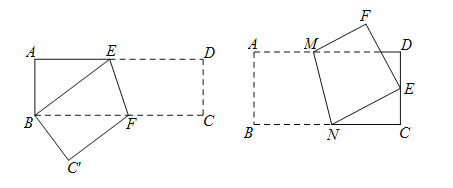
(1)如图,在矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点D与点B重合,折痕为EF,则等腰三角形是 ;
(2)利用勾股定理建立方程,求出BF的长是多少?
(3)拓展:将此矩形折叠,使点B与DC的中点E重合,请你利用添加辅助线的方法,求AM的长;
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形 ABCD 中,对角线 AC、BD 相交于点 O,过点 D 作对角线 BD 的垂线交 BA 的延长线于点 E.
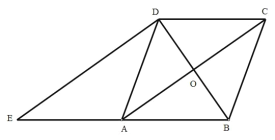
(1)证明:四边形 ACDE 是平行四边形;(2)若 AC=24,BD=18,求△ADE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1930年,德国汉堡大学的学生考拉兹,曾经提出过这样一个数学猜想:对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”,又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明,但举例验证都是正确的,例如:取正整数5,最少经过下面5步运算可得1,即:![]() 如果正整数
如果正整数![]() 最少经过6步运算可得到1,则
最少经过6步运算可得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对该校七年级(1)班全体学生的血型做了一次全面调查,根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
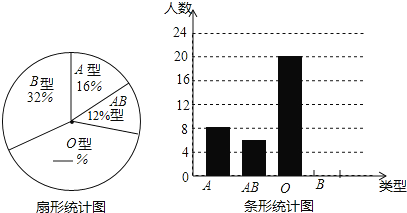
(1)该校七年级(1)班有多少名学生.
(2)求出扇形统计图中“O型”血所对扇形的圆心角的度数.
(3)将条形统计图中“B型”血部分的条形图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外学习时间情况,随机抽取部分学生进行问卷调查,并将调查结果分为 A,B,C,D 四个等级.设学习时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2 ,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
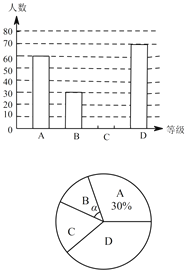
(1)该校共调查了多少名学生;
(2)将条形统计图补充完整;
(3)求出表示 B等级的扇形圆心角 α 的度数;
(4)在此次问卷调查中,甲班有 2 人平均每天课外学习时间超过 2 小时,乙班有 3 人平均每天课外学习时间超过 2 小时,若从这 5 人中任选 2人去参加座谈,试用列表或画树状图的方法求选出的2人
来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.
(1)求一个篮球和一个足球的售价各是多少元?
(2)学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
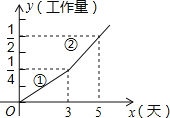
【题目】某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系:
(1)求出图象中②部分的解析式,并求出完成此项工程共需的天数;
(2)该工程共支付8万元,若按完成的工作量所占比例支付工资,甲工程队应得多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com