
【题目】某网店以每件80元的进价购进某种商品,原来按每件100元的售价出售,一天可售出50件;后经市场调查,发现这种商品每件的售价每降低2元,其销售量可增加10件.
(1)该网店销售该商品原来一天可获利润 元.
(2)设后来该商品每件售价降价![]() 元,网店一天可获利润
元,网店一天可获利润![]() 元.
元.
①若此网店为了尽可能增加该商品的销售量,且一天仍能获利1080元,则每件商品的售价应降价多少元?
②求![]() 与
与![]() 之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
【答案】(1)1000;(2)①8;②95;1125
【解析】
(1)用每件利润乘以50件即可;
(2)每件售价降价x元,则每件利润为(100﹣80﹣x)元,销售量为(50+5x)件,它们的乘积为利润y,
①利用y=1080得到方程(100﹣80﹣x)(50+5x)=1080,然后解方程即可;
②由于y=(100﹣80﹣x)(50+5x),则可利用二次函数的性质确定最大利润值.
解:(1)该网店销售该商品原来一天可获利润为(100﹣80)×50=1000(元),
故答案为1000;
(2)①y=(100﹣80﹣x)(50+5x)=﹣5x2+50x+1000,
当y=1080时,﹣5x2+50x+1000=1080,
整理得x2﹣10x+16=0,解得x1=2,x2=8,
答:每件商品的售价应降价2元或8元;
②y=(100﹣80﹣x)(50+5x)=﹣5x2+50x+1000=﹣5(x﹣5)2+1125,
当x=5时,y有最大值,最大值为1125,
则100﹣x=95,
答:当该商品每件售价为95元时,该网店一天所获利润最大,最大利润值为1125元.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某社区计划对面积为1200m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数解析式;
(3)在(2)的情况下,若甲队绿化费用为1600元/天,乙队绿化费用为700元/天,在施工过程中每天需要支付高温补贴a元(100≤a≤300),且工期不得超过14天,则如何安排甲,乙两队施工的天数,使施工费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三江夜游项目是宁波市月光经济和“三江六岸”景观提升的重要工程,一艘游轮从周宿夜江游船码头到宁波大剧院游船码头顺流而行用40分钟,从宁波大剧院游船码头沿原线返回周宿夜江游船码头用了1小时,已知游轮在静水中的平均速度为8千米/小时,求水流的速度.设水流的速度为x千米/小时,则可列方程为( )
A.40(8-x)=1×(8+x) B.![]() (8+x)=8 C.
(8+x)=8 C.![]() (8+x)=8-x D.
(8+x)=8-x D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
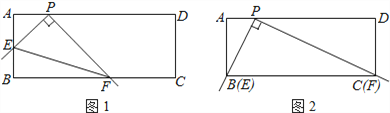
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠ PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
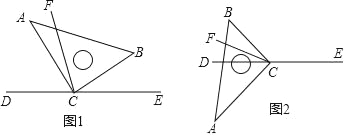
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
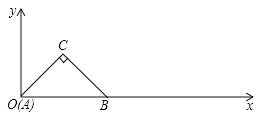
【题目】(3分)在Rt△ABC中,∠C=90°,AC=BC=1,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,△ABC沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽销售渠道,某水果商店计划将146个柚子和400个橙子装入大、小两种礼箱进行出售,其中每件小礼箱装2个柚子和4个橙子;每件大礼箱装3个柚子和9个橙子.要求每件礼箱都装满,柚子恰好全部装完,橙子有剩余,设小礼箱的数量为x件.
(1)大礼箱的数量为________件(用含x的代数式表示).
(2)若橙子剩余12个,则需要大、小两种礼箱共多少件?
(3)由于橙子有剩余,则小礼箱至少需要________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
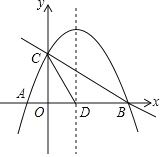
【题目】如图,抛物线![]() 与x轴交于
与x轴交于![]() 、B两点,与y轴交于点
、B两点,与y轴交于点![]() ,抛物线的对称轴交x轴于点D.
,抛物线的对称轴交x轴于点D.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 求
求![]() 的值;
的值;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
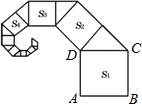
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
A. (![]() )2013B. (
)2013B. (![]() )2014C. (
)2014C. (![]() )2013D. (
)2013D. (![]() )2014
)2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com