Question

【题目】如图， 是⊙ 的直径， 是⊙ 的弦，过点 的切线交 的延长线于点 ，且 .

（1）求 的度数;
（2）若 =3，求图中阴影部分的面积.

Answer 1

【答案】
（1）解：连接OC，

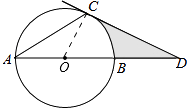
∵过点C的切线交AB的延长线于点D，

∴OC⊥CD，

∴∠OCD=90°，即∠D+∠COD=90°，

∵AO=CO，

∴∠A=∠ACO，

∴∠COD=2∠A，

∵∠A=∠D，

∴∠COD=2∠D，

∴3∠D=90°，

∴∠D=30°，

∴∠ACD=180°-∠A-∠D=180°-30°-30°=120°

（2）解：由（1）可知∠COD=60°在Rt△COD中，∵CD=3，∴OC=3× ，∴阴影部分的面积=

【解析】（1）根据切线的性质和已知∠A=∠D，得到∠COD=2∠D，根据三角形内角和定理，求出∠ACD的度数；（2）由（1）可知∠COD=60°，求出阴影部分的面积等于三角形COD的面积-扇形COB的面积.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案，需要熟知切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．