
【题目】我市创全国卫生城市,某街道积极响应,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍.
![]() 求温馨提示牌和垃圾箱的单价各是多少元?
求温馨提示牌和垃圾箱的单价各是多少元?
![]() 如果该街道需购买温馨提示牌和垃圾箱共3000个.
如果该街道需购买温馨提示牌和垃圾箱共3000个.
![]() 求购买温馨提示牌和垃圾箱所需费用
求购买温馨提示牌和垃圾箱所需费用![]() 元
元![]() 与温馨提示牌的个数x的函数关系式;
与温馨提示牌的个数x的函数关系式;
![]() 若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的
若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的![]() 倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
【答案】(1) 50元和150元;(2)①![]() ;②见解析.
;②见解析.
【解析】
(1)根据购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍,可以列出相应的一元一次方程,从而可以解答本题;
(2)①根据题意可以写出w与x的函数关系式;
②根据题意可以得到关于x的不等式组,从而可以求得x的取值范围,再根据一次函数的性质即可得到所需资金最少的方案,并求出最少需要多少元.
解:![]() 设温馨提示牌的单价为a元,
设温馨提示牌的单价为a元,![]()
解得:![]() ,
,
则![]() ,
,
答:温馨提示牌、垃圾箱的单价分别为50元和150元;![]() 由题意可得,
由题意可得,![]() ,
,
即购买温馨提示牌和垃圾箱所需费用![]() 元
元![]() 与温馨提示牌的个数x的函数关系式是:
与温馨提示牌的个数x的函数关系式是:![]() ;
;![]() 由题意得,
由题意得,![]() ,
,
解得:![]() ,
,![]() 为整数,
为整数,![]() 共有201种可供选择的方案,
共有201种可供选择的方案,![]() ,w随x的增大而减小,
,w随x的增大而减小,![]() 当
当![]() 时,w取得最小值,此时
时,w取得最小值,此时![]() 元,
元,![]() ,
,
答:有201种可供选择的方案,其中购买温馨提示牌1200个,垃圾桶1800个时所需资金最少,最少为330000元.


科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,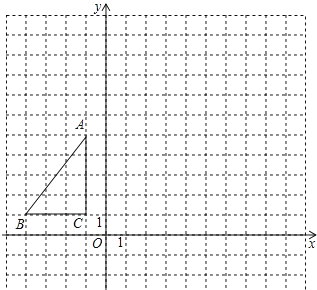
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程,并在括号中填上理论依据.
如图,已知AC⊥AE垂足为A,BD⊥BF垂足为B,∠1=35°,∠2=35°.

证明:AC∥BD; AE∥BF.
证明:∵∠1=∠2=35°,
∴ ∥ ( )
∵AC⊥AE,BD⊥BF,
∴∠ =∠ =90°
又∵∠1=∠2=35°,
∴∠ =∠
∴EA∥BF( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, BD是∠ABC的平分线,过点C作CE⊥BD,交 BD的延长线于点E,∠ABC=60°,∠ECD=15°.
(1)直接写出∠ADB的度数是_______;
(2)求证:BD=AB;
(3)若AB=2,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查发现:在一段时间内,当销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.若商场要获得10000元销售利润,该玩具销售单价应定为多少元?售出玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
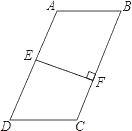
【题目】如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
(1)若AB=DC,则四边形ABCD的面积S=__;
(2)若AB>DC,则此时四边形ABCD的面积S′__S(用“>”或“=”或“<”填空).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com