
【题目】如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,E点是BC的中点,F是AB延长线上一点且FB=1.
(1)求经过点O,A,E三点的抛物线解析式;
(2)点P在抛物线上运动,当点P运动到什么位置时△OAP的面积为2,请求出点P的坐标;
(3)在抛物线上是否存在一点Q,使△AFQ是等腰直角三角形?若存在直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:A的坐标是(2,0),E的坐标是(1,2).
设抛物线的解析式是y=ax2+bx+c,
根据题意得:  ,
,
解得: 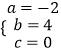 .
.
则抛物线的解析式是y=﹣2x2+4x

(2)解:当△OAP的面积是2时,P的纵坐标是2或﹣2.
当﹣2x2+4x=2时,解得:x=1,则P的坐标是(1,2);
当﹣2x2+4x=﹣2时,解得:x=1± ![]() ,
,
此时P的坐标是(1+ ![]() ,﹣2)或(1﹣
,﹣2)或(1﹣ ![]() ,﹣2)
,﹣2)
(3)解:AF=AB+BF=2+1=3.
OA=2,则A是直角顶点时,Q不可能在抛物线上;
当F是直角顶点时,Q不可能在抛物线上;
当Q是直角顶点时,Q到AF的距离是 ![]() AF=
AF= ![]() ,若Q存在,则Q的坐标是(2﹣
,若Q存在,则Q的坐标是(2﹣ ![]() ,
, ![]() ),即(
),即( ![]() ,
, ![]() ),在抛物线上;
),在抛物线上;
综上,抛物线上存在Q点满足题目要求
【解析】(1)先求出A、O、E三点的坐标,利用待定系数法代入解析式即可;(2)因为OA=2,所以当△OAP的面积是2时,就是P到x轴的距离是2,即P的纵坐标是2或﹣2,即﹣2x2+4x=2或2x2+4x=﹣2解方程;(3)△AFQ是等腰直角三角形可分类讨论:A是直角顶点;F是直角顶点;Q是直角顶点;


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,已知![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)填空:![]() = _____ ,
= _____ ,![]() = _____ ;
= _____ ;
(2)如果在第三象限内一点![]() ,请用含
,请用含![]() 的式子表示⊿
的式子表示⊿![]() 的面积;
的面积;
(3)若⑵条件下,当![]() 时,在坐标轴上一点
时,在坐标轴上一点![]() ,使得⊿
,使得⊿![]() 的面积与⊿
的面积与⊿![]() 的面积相等,请求出点
的面积相等,请求出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在全校学生中开展了“地球﹣我们的家园”为主题的环保征文比赛,评选出一、二、三等奖和优秀奖,根据奖项的情况绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)该校获奖的总人数为 , 并把条形统计图补充完整;
(2)求在扇形统计图中表示“二等奖”的扇形的圆心角的度数;
(3)获得一等奖的4名学生中有3男1女,现打算从中随机选出2名学生参加颁奖活动,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程,并在括号内填上依据.
如图,点E在AB上,点F在CD上,∠1=∠2,∠B=∠C,求证AB∥CD.
证明:∵∠1=∠2(已知),∠1=∠4( ),
∴∠2= (等量代换),
∴ ∥BF( ),
∴∠3=∠ ( ).
又∵∠B=∠C(已知),
∴∠3=∠B( ),
∴AB∥CD( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com