练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

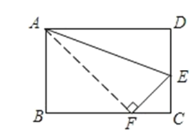
    【题目】如图，四边形ABCD是一个矩形，BC=10cm，AB=8cm。现沿AE折叠，使点D恰好落在BC边上的点F处，求：（1）BF的长；（2）CE的长.

    【答案】(1)6;(2)3.

    【解析】

    （1）根据折叠的性质得AF=AD=10,在直角三角形ABF利用勾股定理即可证明；（2）

    由EF＝DE＝CD-CE＝8-CE，CF＝BC-BF＝4在Rt△EFC中利用EF＝CF+CE，即（8-CE）＝16+CE，即可求出CE的长.

    解：∵矩形ABCD
    ∴AD＝BC＝10,CD＝AB＝8, ∠B＝∠C＝∠D＝90
    ∵△ADE沿AE折叠至△AFE
    ∴AF＝AD＝10,EF＝DE＝CD-CE＝8-CE
    ∴BF＝==6
    ∴CF＝BC-BF＝10-6＝4
    ∵EF＝CF+CE
    ∴（8-CE）＝16+CE
    ∴CE＝3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，三角形(记作)在方格中，方格纸中的每个小方格都是边长为1个单位的正方形，三个顶点的坐标分别是，，，先将向上平移3个单位长度，再向右平移2个单位长度，得到.

    (1)在图中画出；

    (2)点，，的坐标分别为______、________、_________；

    (3)若有一点，使与面积相等，求出点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数的图像与x轴交于点A(-1,0)、B（3，0），与y轴交于点C（0，3）.

    （1）求二次函数的表达式；

    （2）设上述抛物线的对称轴l与x轴交于点D，过点C作CE⊥l于E，P为线段DE上一点，Q(m，0)为x轴负半轴上一点，以P、Q、D为顶点的三角形与△CPE相似；

    ①当满足条件的点有且只有三个时，求的取值范围；

    ②若满足条件的点有且只有两个，直接写出的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】科技人员研制出采摘水果的单人便携式采摘机，已知雇一个工手工采摘每小时可采摘水果10公斤，一个雇工操作该采摘机每小时可摘水果35公斤，雇工每天工作8小时.

    （1）一个雇工手工采摘水果，一天能采摘_______公斤.

    （2）张家和王家均雇人采摘水果，王家雇的人数是张家的2倍，张家的人手工采摘，王家所雇的人中的用采摘机采摘，用手工采摘.已知手工采摘1公斤水果的费用是1.5元，设张家雇佣人.

    ①用含的代数式表示：

    王家雇佣的人数：_________人；王家雇佣的人中用采摘机采摘人数：__________人.

    ②张家付给雇工一天的工资总额为1440元，求的值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线y=﹣x+2与反比例函数y=的图象有唯一公共点，若直线y=﹣x+b与反比例函数y=的图象有2个公共点，则b的取值范围是（　　）

    A. b＞2 B. ﹣2＜b＜2 C. b＞2或b＜﹣2 D. b＜﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的对角线AC、BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，A′B′交BC于点E，A′D′交CD于点F.

    （1）求证：OE=OF；

    （2）若正方形ABCD的边长为1，求两个正方形重叠部分的面积；

    （3）若正方形 A′B′C′D′绕着O点旋转，EF的长度何时最小，并求出最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

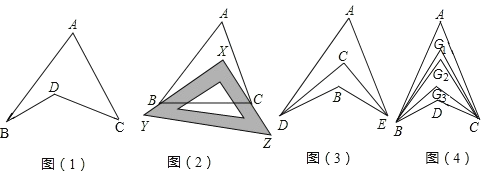
    【题目】探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”．

    （1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；

    （2）请你直接利用以上结论，解决以下三个问题：

    ①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A=40°，则∠ABX+∠ACX=　 　°；

    ②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=40°，∠DBE=130°，求∠DCE的度数；

    ③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC=133°，∠BG1C=70°，求∠A的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列事件中是不可能事件的是（　　）

    A. 任意画一个四边形，它的内角和是

    B. 若，则

    C. 一只不透明的袋子共装有3个小球，它们的标号分别为1、2、3，从中摸出一个小球，标号是“5”

    D. 掷一枚质地均匀的硬币，落地时正面朝上

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某修理厂需要购进甲、乙两种配件，经调查，每个甲种配件的价格比每个乙种配件的价格少0.4万元，且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同．

    （1）求每个甲种配件、每个乙种配件的价格分别为多少万元；

    （2）现投入资金80万元，根据维修需要预测，甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件．

    查看答案和解析>>

    同步练习册答案