
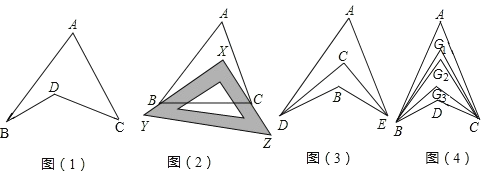
”¾ĢāÄæ”æĢ½¾æÓė·¢ĻÖ£ŗČēĶ¼1ĖłŹ¾µÄĶ¼ŠĪ£¬ĻńĪŅĆĒ³£¼ūµÄѧĻ°ÓĆĘ·©©Ō²¹ę£®ĪŅĆĒ²»·Į°ŃÕāŃłĶ¼ŠĪ½Š×ö”°¹ęŠĪĶ¼”±£®
£Ø1£©¹Ū²ģ”°¹ęŠĪĶ¼”±£¬ŹŌĢ½¾æ”ĻBDCÓė”ĻA”¢”ĻB”¢”ĻCÖ®¼äµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ĒėÄćÖ±½ÓĄūÓĆŅŌÉĻ½įĀŪ£¬½ā¾öŅŌĻĀČżøöĪŹĢā£ŗ
¢ŁČēĶ¼2£¬°ŃŅ»æéČż½Ē³ßXYZ·ÅÖĆŌŚ”÷ABCÉĻ£¬Ź¹Čż½Ē³ßµÄĮ½ĢõÖ±½Ē±ßXY”¢XZĒ”ŗĆ¾¹żµćB”¢C£¬”ĻA=40”ć£¬Ōņ”ĻABX+”ĻACX=”” ”””ć£»
¢ŚČēĶ¼3£¬DCĘ½·Ö”ĻADB£¬ECĘ½·Ö”ĻAEB£¬Čō”ĻDAE=40”ć£¬”ĻDBE=130”ć£¬Ēó”ĻDCEµÄ¶ČŹż£»
¢ŪČēĶ¼4£¬”ĻABD£¬”ĻACDµÄ10µČ·ÖĻßĻą½»ÓŚµćG1”¢G2””¢G9£¬Čō”ĻBDC=133”ć£¬”ĻBG1C=70”ć£¬Ēó”ĻAµÄ¶ČŹż£®
”¾“š°ø”æ£Ø1£©”ĻBDC=”ĻA+”ĻB+”ĻC£»£Ø2£©¢Ł50”ć£»¢Ś85”ć£»¢Ū63”ć.
”¾½āĪö”æ
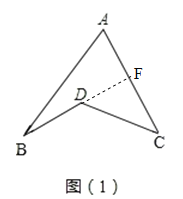
£Ø1£©ŃÓ³¤BD½»ACÓŚF£¬øł¾ŻĶā½ĒµÄŠŌÖŹ£¬¼“æÉÅŠ¶Ļ³ö”ĻBDC=”ĻBAC+”ĻB+”ĻC£®
£Ø2£©¢ŁÓÉ£Ø1£©æɵƔĻABX+”ĻACX+”ĻA=”ĻBXC£¬Č»ŗóøł¾Ż”ĻA=40”ć£¬”ĻBXC=90”ć£¬¼“æÉĒó³ö”ĻABX+”ĻACXµÄÖµ£®
¢ŚÓÉ£Ø1£©æɵƔĻDBE=”ĻDAE+”ĻADB+”ĻAEB£¬ŌŁøł¾Ż”ĻDAE=40”ć£¬”ĻDBE=130”ć£¬Ēó³ö”ĻADB+”ĻAEBµÄÖµ£»Č»ŗóøł¾Ż”ĻDCE![]() £Ø”ĻADB+”ĻAEB£©+”ĻDAE£¬¼“æÉĒó³ö”ĻDCEµÄ¶ČŹż£®
£Ø”ĻADB+”ĻAEB£©+”ĻDAE£¬¼“æÉĒó³ö”ĻDCEµÄ¶ČŹż£®
¢Ūøł¾Ż”ĻBG1C![]() £Ø”ĻABD+”ĻACD£©+”ĻA£¬”ĻBG1C=70”ć£¬Éč”ĻAĪŖx”ć£¬æɵƔĻABD+”ĻACD=133”ć©x”ć£¬½ā·½³Ģ£¬Ēó³öxµÄÖµ£¬¼“æÉÅŠ¶Ļ³ö”ĻAµÄ¶ČŹż£®
£Ø”ĻABD+”ĻACD£©+”ĻA£¬”ĻBG1C=70”ć£¬Éč”ĻAĪŖx”ć£¬æɵƔĻABD+”ĻACD=133”ć©x”ć£¬½ā·½³Ģ£¬Ēó³öxµÄÖµ£¬¼“æÉÅŠ¶Ļ³ö”ĻAµÄ¶ČŹż£®
£Ø1£©ČēĶ¼£Ø1£©£¬ŃÓ³¤BD½»ACÓŚF£¬øł¾ŻĶā½ĒµÄŠŌÖŹ£¬æÉµĆ£ŗ”ĻDFC=”ĻA+”ĻB£®
”ß”ĻBDC=”ĻDFC+”ĻC£¬”ą”ĻBDC=”ĻA+”ĻB+”ĻC£»
£Ø2£©¢ŁÓÉ£Ø1£©£¬æÉµĆ£ŗ”ĻABX+”ĻACX+”ĻA=”ĻBXC£®
”ß”ĻA=40”ć£¬”ĻBXC=90”ć£¬”ą”ĻABX+”ĻACX=90”ć©40”ć=50”ć£®
¹Ź“š°øĪŖ£ŗ50£®
¢ŚÓÉ£Ø1£©£¬æÉµĆ£ŗ”ĻDBE=”ĻDAE+”ĻADB+”ĻAEB£¬”ą”ĻADB+”ĻAEB=”ĻDBE©”ĻDAE=130”ć©40”ć=90”ć£¬”ą![]() £Ø”ĻADB+”ĻAEB£©=90”ć”Ā2=45”ć£¬”ą”ĻDCE
£Ø”ĻADB+”ĻAEB£©=90”ć”Ā2=45”ć£¬”ą”ĻDCE![]() £Ø”ĻADB+”ĻAEB£©+”ĻDAE=45”ć+40”ć=85”ć£»
£Ø”ĻADB+”ĻAEB£©+”ĻDAE=45”ć+40”ć=85”ć£»
¢Ū”ĻBG1C![]() £Ø”ĻABD+”ĻACD£©+”ĻA£®
£Ø”ĻABD+”ĻACD£©+”ĻA£®
”ß”ĻBG1C=70”ć£¬”ąÉč”ĻAĪŖx”ć£®
”ß”ĻABD+”ĻACD=133”ć©x”ć
”ą![]() £Ø133©x£©+x=70£¬”ą13.3
£Ø133©x£©+x=70£¬”ą13.3![]() x+x=70£¬½āµĆ£ŗx=63£¬¼“”ĻAµÄ¶ČŹżĪŖ63”ć£®
x+x=70£¬½āµĆ£ŗx=63£¬¼“”ĻAµÄ¶ČŹżĪŖ63”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy1=x+bÓėĖ«ĒśĻßy2=![]() ½»ÓŚµćA£Ø1£¬4£©ŗĶµćB£¬¾¹żµćAµÄĮķŅ»ĢõÖ±ĻßÓėĖ«ĒśĻßy2=
½»ÓŚµćA£Ø1£¬4£©ŗĶµćB£¬¾¹żµćAµÄĮķŅ»ĢõÖ±ĻßÓėĖ«ĒśĻßy2=![]() ½»ÓŚµćC£®Ōņ£ŗ
½»ÓŚµćC£®Ōņ£ŗ
¢ŁÖ±ĻßABµÄ½āĪöŹ½ĪŖy1=x+3£»
¢ŚB£Ø©1£¬©4£©£»
¢Ūµ±x£¾1Ź±£¬y2£¼y1£»
¢Üµ±ACµÄ½āĪöŹ½ĪŖy=4xŹ±£¬”÷ABCŹĒÖ±½ĒČż½ĒŠĪ£®
ĘäÖŠÕżČ·µÄŹĒ £®£Ø°ŃĖłÓŠÕżČ·½įĀŪµÄŠņŗŶ¼Š“ŌŚŗįĻßÉĻ£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬OĪŖ×ų±źĻµŌµć£¬A£Ø3£¬0£©£¬B£Ø3£¬1£©£¬C£Ø0£¬1£©£¬½«”÷OABŃŲÖ±ĻßOBÕŪµž£¬Ź¹µĆµćAĀäŌŚµćD“¦£¬ODÓėBC½»ÓŚµćE£¬ŌņODĖłŌŚÖ±ĻߵĽāĪöŹ½ĪŖ£Ø””””£©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
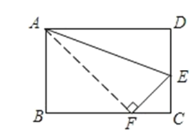
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDŹĒŅ»øö¾ŲŠĪ£¬BC=10cm£¬AB=8cm”£ĻÖŃŲAEÕŪµž£¬Ź¹µćDĒ”ŗĆĀäŌŚBC±ßÉĻµÄµćF“¦£¬Ēó£ŗ£Ø1£©BFµÄ³¤£»£Ø2£©CEµÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬MNŹĒ”ŃOµÄÖ±¾¶£¬×÷AB”ĶMN£¬“¹×ćĪŖµćD£¬Į¬½ÓAM£¬AN£¬µćCĪŖ![]() ÉĻŅ»µć£¬ĒŅ
ÉĻŅ»µć£¬ĒŅ![]() £¬Į¬½ÓCM£¬½»ABÓŚµćE£¬½»ANÓŚµćF£¬ĻÖøų³öŅŌĻĀ½įĀŪ£ŗ¢ŁAD=BD£»¢Ś”ĻMAN=90”ć£»¢Ū
£¬Į¬½ÓCM£¬½»ABÓŚµćE£¬½»ANÓŚµćF£¬ĻÖøų³öŅŌĻĀ½įĀŪ£ŗ¢ŁAD=BD£»¢Ś”ĻMAN=90”ć£»¢Ū![]() £»¢Ü”ĻACM+”ĻANM=”ĻMOB£»¢ŻAE=
£»¢Ü”ĻACM+”ĻANM=”ĻMOB£»¢ŻAE=![]() MF£®
MF£®
ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø””””£©

A. 2 B. 3 C. 4 D. 5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬ADŗĶBEŹĒøߣ¬”ĻABE=45”ć£¬µćFŹĒABµÄÖŠµć£¬ADÓėFE”¢BE·Ö±š½»ÓŚµćG”¢H£¬”ĻCBE=”ĻBAD£®ÓŠĻĀĮŠ½įĀŪ£ŗ¢ŁFD=FE£»¢ŚAH=2CD£»¢ŪBCAD=![]() AE2£»¢ÜS”÷ABC=4S”÷ADF£®ĘäÖŠÕżČ·µÄÓŠ£Ø £©
AE2£»¢ÜS”÷ABC=4S”÷ADF£®ĘäÖŠÕżČ·µÄÓŠ£Ø £©
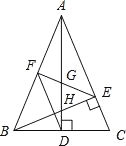
A£®1øö B£®2 øö C£®3 øö D£®4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾ĪŖŅ»øö¼ĘĖć³ĢŠņ

(1)ČōŹäČėµÄx£½3£¬ŌņŹä³öµÄ½į¹ūĪŖ”ų
(2)ČōæŖŹ¼ŹäČėµÄxĪŖÕżÕūŹż£¬×īŗóŹä³öµÄ½į¹ūĪŖ40£¬ŌņĀś×ćĢõ¼žµÄxµÄ²»Ķ¬Öµ×ī¶ąÓŠ”÷øö
(3)¹ę¶Ø:³ĢŠņŌĖŠŠµ½”°ÅŠ¶Ļ½į¹ūŹĒ·ń“óÓŚ0£¢ĪŖŅ»“ĪŌĖĖć.ČōŌĖĖć½ųŠŠĮĖČż“Ī²ÅŹä³ö£¬ĒóxµÄȔֵ·¶Ī§”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£ŗ½«±ß³¤ĪŖ1µÄÕżČż½ĒŠĪOAP£¬ŃŲxÖįÕż·½ĻņĮ¬Šų·×ŖČōøÉ“Ī£¬µćAŅĄ“ĪĀäŌŚµćA1£¬A2£¬A3£¬A4£¬”£¬A2019µÄĪ»ÖĆÉĻ£¬ŌņµćA2019µÄ×ų±źĪŖ______£®
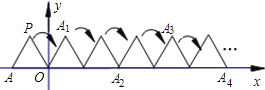
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ±ćÓŚ¹ÜĄķÓė³”µŲ°²ÅÅ£¬Ėɱ±Ä³ÖŠŃ§Š£ŅŌŠ”Ć÷ĖłŌŚ°ą¼¶ĪŖĄż£¬¶Ōѧɜ²Ī¼Óø÷øöĢåÓżĻīÄæ½ųŠŠĮĖµ÷²éĶ³¼Ę£®²¢°Ńµ÷²éµÄ½į¹ū»ęÖĘĮĖČēĶ¼ĖłŹ¾µÄ²»ĶźČ«Ķ³¼ĘĶ¼£¬ĒėÄćøł¾ŻĻĀĮŠŠÅĻ¢»Ų“šĪŹĢā£ŗ

£Ø1£©ŌŚÕā“Īµ÷²éÖŠ£¬Š”Ć÷ĖłŌŚµÄ°ą¼¶²Ī¼ÓĄŗĒņĻīÄæµÄĶ¬Ń§ÓŠ¶ąÉŁČĖ£æ²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£®
£Ø2£©Čē¹ūѧŠ£ÓŠ800Ćūѧɜ£¬Ēė¹Ą¼ĘČ«Š£Ń§ÉśÖŠÓŠ¶ąÉŁČĖ²Ī¼ÓĄŗĒņĻīÄ森
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com