【题目】如图，直线y1=x+b与双曲线y2=
交于点A（1，4）和点B，经过点A的另一条直线与双曲线y2=交于点C．则：
①直线AB的解析式为y1=x+3；
②B（﹣1，﹣4）；
③当x＞1时，y2＜y1；
④当AC的解析式为y=4x时，△ABC是直角三角形．
其中正确的是 ．（把所有正确结论的序号都写在横线上）
【答案】①③④．
【解析】
试题分析：∵直线y1=x+b与双曲线y2=
交于点A（1，4），∴4=1+b，4=
，∴b=3，k=4，
∴直线AB的解析式为y1=x+3，双曲线的解析式为y2=
，故①正确；
把y1=x+3代入y2=，得x+3=，整理得，x2+3x﹣4=0，解得x=﹣4或1，当x=﹣4时，y1=﹣4+3=﹣1，∴B点坐标为（﹣4，﹣1），故②错误；
由图象可知，y2＜y1时，﹣4＜x＜0或x＞1，∴当x＞1时，y2＜y1，故③正确；
当AC的解析式为y=4x时，把y=4x代入y2=，得4x=，整理得，4x2=4，
解得x=±1，当x=﹣1时，y=﹣4，∴C（﹣1，﹣4）．∵A（1，4），B（﹣4，﹣1），C（﹣1，﹣4），∴AB2=（﹣4﹣1）2+（﹣1﹣4）2=50，BC2=（﹣1+4）2+（﹣4+1）2=18，AC2=（﹣1﹣1）2+（﹣4﹣4）2=68，∴AB2+BC2=AC2，∴△ABC是直角三角形．
则正确的结论是①③④．
A加金题 系列答案
全优测试卷系列答案科目：初中数学 来源： 题型：
【题目】请将下列证明过程补充完整：
已知：如图，AE平分∠BAC，CE平分∠ACD,且∠α＋∠β＝90°.
求证：AB∥CD.
证明：∵CE平分∠ACD (已知），
∴∠ACD＝2∠α(______________________)
∵AE平分∠BAC (已知)，
∴∠BAC＝_________(______________________)
∵∠α＋∠β＝90°（已知），
∴2∠α＋2∠β＝180°（等式的性质）
∴∠ACD＋∠BAC＝＝_________(______________________)
∴AB∥CD.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在直角坐标系中，已知A（0，a），B（b，0）C（3，c）三点，若a，b，c满足关系式：|a﹣2|+（b﹣3）2+
＝0．
（1）求a，b，c的值．
（2）求四边形AOBC的面积．
（3）是否存在点P（x，﹣
x），使△AOP的面积为四边形AOBC的面积的两倍？若存在，求出点P的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，三角形
(记作
)在方格中，方格纸中的每个小方格都是边长为1个单位的正方形，三个顶点的坐标分别是
，
，
，先将向上平移3个单位长度，再向右平移2个单位长度，得到
.
(1)在图中画出
；
(2)点
，
，
的坐标分别为______、________、_________；
(3)若
有一点
，使
与面积相等，求出点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2018年4月23日，第23个世界读书日．为了推进中华传统文化教育，营造浓郁的读书氛围，我区某学校举办了“让读书成为习惯，让书香飘满校园”主题活动，为此特为每个班级订购了一批新的图书．初二年级两个班订购图书情况如下表：
老舍文集（套） | 四大名著（套） | 总费用（元） | |
初二（1）班 | 4 | 2 | 480 |
初二（2）班 | 2 | 3 | 520 |
（1）求老舍文集和四大名著每套各是多少元；
（2）学校准备再购买老舍文集和四大名著共10套，总费用不超过700元，问学校有哪几种购买方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
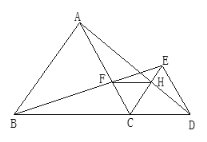
【题目】如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，
(1)求证：△BCE≌△ACD；
(2)求证：FC=HC
(3)求证：FH∥BD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公交车每月的支出费用为4000元，每月的乘车人数
(人)与每月利润(利润=收入费用-支出费用)
(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的)；
(1)在这个变化过程中， 是自变量， 是因变量；(填中文)
(2)观察表中数据可知，每月乘客量达到 人以上时，该公交车才不会亏损；
(3)请你估计当每月乘车人数为3500人时，每月利润为 元？
(4)若5月份想获得利润5000元，则请你估计5月份的乘客量需达 人.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图像与x轴交于点A(-1,0)、B（3，0），与y轴交于点C（0，3）.
（1）求二次函数的表达式；
（2）设上述抛物线的对称轴l与x轴交于点D，过点C作CE⊥l于E，P为线段DE上一点，Q(m，0)为x轴负半轴上一点，以P、Q、D为顶点的三角形与△CPE相似；
①当满足条件的
点有且只有三个时，求
的取值范围；
②若满足条件的
点有且只有两个，直接写出
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
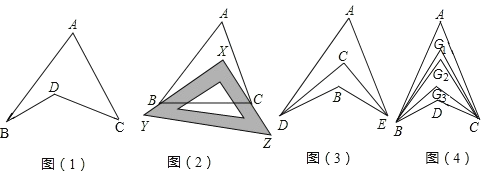
【题目】探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”．
（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；
（2）请你直接利用以上结论，解决以下三个问题：
①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A=40°，则∠ABX+∠ACX= °；
②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=40°，∠DBE=130°，求∠DCE的度数；
③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC=133°，∠BG1C=70°，求∠A的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com