
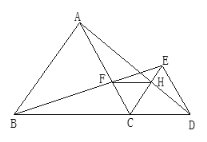
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
(1)求证:△BCE≌△ACD;
(2)求证:FC=HC
(3)求证:FH∥BD.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)先根据△ABC和△CDE都是等边三角形得出BC=AC,CE=CD,∠BCA=∠ECD=60°,再由SAS定理即可得出△BCE≌△ACD;
(2)由△BCE ≌ △ACD,可得∠CBF=∠CAH,然后根据“ASA”证明△BCF≌△ACH即可;
(3)根据∠FCH=60°,可知△CHF为等边三角形,进而可得出结论.
(1)∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠BCA=∠ECD=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴在△BCE和△ACD中,
BC=AC∠BCE=∠ACDCE=CD,
∴△BCE ≌ △ACD(SAS).
(2)∵△BCE ≌ △ACD,
∴∠CBF=∠CAH,
又∵△ABC和△CDE都是等边三角形,且点B、C、D在同一条直线上,
∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF,
在△BCF和△ACH中,
∠CBE=∠CAHBC=AC∠BCF=∠ACH,
∴△BCF≌△ACH(ASA),
∴CF=CH,
(3)∵∠FCH=60°,
∴△CHF为等边三角形
∴∠FHC=∠HCD=60°,
∴FH∥BD.


科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与
于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与![]() 、
、![]() 交于点C、D,连接AD、BC.
交于点C、D,连接AD、BC.
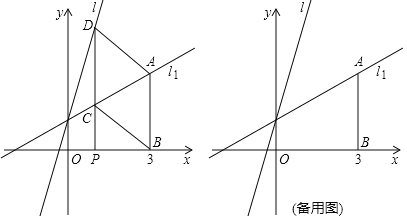
![]() 直接写出线段
直接写出线段![]() ______;
______;
![]() 当P的坐标是
当P的坐标是![]() 时,求直线BC的解析式;
时,求直线BC的解析式;
![]() 若
若![]() 的面积与
的面积与![]() 的面积相等,求点P的坐标.
的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市“上品”房地产开发公司于2010年5月份完工一商品房小区,6月初开始销售,其中6月的销售单价为0.7万元/m2,7月的销售单价为0.72万元/m2,且每月销售价格y1(单位:万元/m2)与月份x(6≤x≤11,x为整数)之间满足一次函数关系:每月的销售面积为y2(单位:m2),其中y2=﹣2000x+26000(6≤x≤11,x为整数).
(1)求y1与月份x的函数关系式;
(2)6~11月中,哪一个月的销售额最高?最高销售额为多少万元?
(3)2010年11月时,因会受到即将实行的“国八条”和房产税政策的影响,该公司销售部预计12月份的销售面积会在11月销售面积基础上减少20a%,于是决定将12月份的销售价格在11月的基础上增加a%,该计划顺利完成.为了尽快收回资金,2011年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为4618.4万元,请根据以上条件求出a的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=x+b与双曲线y2=![]() 交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=
交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=![]() 交于点C.则:
交于点C.则:
①直线AB的解析式为y1=x+3;
②B(﹣1,﹣4);
③当x>1时,y2<y1;
④当AC的解析式为y=4x时,△ABC是直角三角形.
其中正确的是 .(把所有正确结论的序号都写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
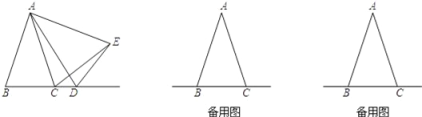
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)下表是2008年北京奥运会部分国家金牌榜:
国家 | 中国 | 美国 | 俄罗斯 | 英国 | 德国 | 澳大利亚 | 本届奥运会金牌总数 |
金牌数 | 51 | 36 | 23 | 19 | 16 | 14 | 302 |
①选择 统计图来描述上表中各国金牌数最恰当.请把这个统计图画出来.
②请你根据统计图,写出两条与29届奥运会金牌数有关的信息.
(2)下表是中国奥运代表团自1984年第23届洛杉矶奥运会以来,历届奥运会的金牌总数统计表:
年份 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
金牌数 | 15 | 5 | 16 | 16 | 28 | 32 | 51 |
①选择 统计图来描述上表中我国各届金牌数最恰当.把这个统计图画出来.
②请你根据统计图,写出两条与中国奥运金牌数相关的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的有( )
AE2;④S△ABC=4S△ADF.其中正确的有( )
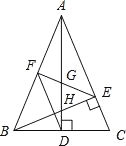
A.1个 B.2 个 C.3 个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com