
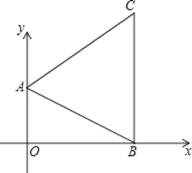
【题目】如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+![]() =0.
=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.

【答案】(1)a=2,b=3,c=4;(2)9;(3)存在点P(18,﹣9)或(﹣18,9),使△AOP的面积为四边形AOBC的面积的两倍.
【解析】
(1)根据“几个非负数相加和为0,则每一个非负数的值均为0”解出a,b,c的值;
(2)由点A、O、B、C的坐标可得四边形AOBC为直角梯形,根据直角梯形的面积公式计算即可;
(3)设存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程
x),使△AOP的面积为四边形AOBC的面积的两倍.根据面积列出方程![]() ×2×|x|=|x|=2×9,解方程即可.
×2×|x|=|x|=2×9,解方程即可.
解:(1)∵|a﹣2|+(b﹣3)2+![]() =0,
=0,
∴a﹣2=0,b﹣3=0,c﹣4=0,
∴a=2,b=3,c=4;
(2)∵A(0,2),O(0,0),B(3,0),C(3,4);
∴四边形AOBC为直角梯形,且OA=2,BC=4,OB=3,
∴四边形AOBC的面积=![]() ×(OA+BC)×OB=
×(OA+BC)×OB=![]() ×(2+4)×3=9;
×(2+4)×3=9;
(3)设存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍.
x),使△AOP的面积为四边形AOBC的面积的两倍.
∵△AOP的面积=![]() ×2×|x|=|x|,
×2×|x|=|x|,
∴|x|=2×9,
∴x=±18
∴存在点P(18,﹣9)或(﹣18,9),
使△AOP的面积为四边形AOBC的面积的两倍.
故答案为:(1)a=2,b=3,c=4;(2)9;(3)存在点P(18,﹣9)或(﹣18,9),使△AOP的面积为四边形AOBC的面积的两倍.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
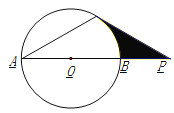
【题目】如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
(1) 求证:CP是⊙O的切线;
(2) 若PC=6,AB=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论(只要写出一条结论).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=x+b与双曲线y2=![]() 交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=
交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=![]() 交于点C.则:
交于点C.则:
①直线AB的解析式为y1=x+3;
②B(﹣1,﹣4);
③当x>1时,y2<y1;
④当AC的解析式为y=4x时,△ABC是直角三角形.
其中正确的是 .(把所有正确结论的序号都写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com