
【题目】如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据矩形的性质结合折叠的性质可得出∠EOB=∠EBO,进而可得出OE=BE,设点E的坐标为(m,1),则OE=BE=3-m,CE=m,利用勾股定理即可求出m值,再根据点E的坐标,利用待定系数法即可求出OD所在直线的解析式.
∵A(3,0),B(3,1),C(0,1),O(0,0),
∴四边形OABC为矩形,
∴∠EBO=∠AOB.
又∵∠EOB=∠AOB,
∴∠EOB=∠EBO,
∴OE=BE,
设点E的坐标为(m,1),则OE=BE=3-m,CE=m,
在Rt△OCE中,OC=1,CE=m,OE=3-m,
∴(3-m)2=12+m2,
∴m=![]() ,
,
∴点E的坐标为(![]() ,1),
,1),
设OD所在直线的解析式为y=kx,
将点E(![]() ,1)代入y=kx中,
,1)代入y=kx中,
得1=![]() k,解得:k=
k,解得:k=![]() ,
,
∴OD所在直线的解析式为y=![]() x.
x.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a﹣2|+(b﹣3)2+![]() =0.
=0.
(1)求a,b,c的值.
(2)求四边形AOBC的面积.
(3)是否存在点P(x,﹣![]() x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.
x),使△AOP的面积为四边形AOBC的面积的两倍?若存在,求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每月的支出费用为4000元,每月的乘车人数![]() (人)与每月利润(利润=收入费用-支出费用)
(人)与每月利润(利润=收入费用-支出费用)![]() (元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);
(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的);

(1)在这个变化过程中, 是自变量, 是因变量;(填中文)
(2)观察表中数据可知,每月乘客量达到 人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为 元?
(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求二次函数的表达式;
(2)设上述抛物线的对称轴l与x轴交于点D,过点C作CE⊥l于E,P为线段DE上一点,Q(m,0)为x轴负半轴上一点,以P、Q、D为顶点的三角形与△CPE相似;
①当满足条件的![]() 点有且只有三个时,求
点有且只有三个时,求![]() 的取值范围;
的取值范围;
②若满足条件的![]() 点有且只有两个,直接写出
点有且只有两个,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球,其中红球有2个,黄球有1个,从中任意摸出1球是红球的概率为![]() .
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技人员研制出采摘水果的单人便携式采摘机,已知雇一个工手工采摘每小时可采摘水果10公斤,一个雇工操作该采摘机每小时可摘水果35公斤,雇工每天工作8小时.
(1)一个雇工手工采摘水果,一天能采摘_______公斤.
(2)张家和王家均雇人采摘水果,王家雇的人数是张家的2倍,张家的人手工采摘,王家所雇的人中的![]() 用采摘机采摘,
用采摘机采摘,![]() 用手工采摘.已知手工采摘1公斤水果的费用是1.5元,设张家雇佣
用手工采摘.已知手工采摘1公斤水果的费用是1.5元,设张家雇佣![]() 人.
人.
①用含![]() 的代数式表示:
的代数式表示:
王家雇佣的人数:_________人;王家雇佣的人中用采摘机采摘人数:__________人.
②张家付给雇工一天的工资总额为1440元,求![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣x+2与反比例函数y=![]() 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=
的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=![]() 的图象有2个公共点,则b的取值范围是( )
的图象有2个公共点,则b的取值范围是( )

A. b>2 B. ﹣2<b<2 C. b>2或b<﹣2 D. b<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
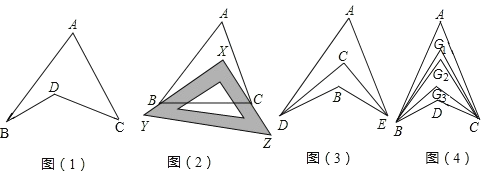
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
初步探究
(1)写出点B的坐标 ;
(2)点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
(3)当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;并求出这个图形所对应的函数表达式.
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com