
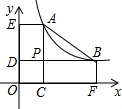
 如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论:
如图,点A,B在双曲线y=$\frac{k}{x}$(x>0)上,分别过点A、B向x轴、y轴作垂线.垂足分别为点C、E、F、D,AC和BD交于点P,$\frac{AP}{PC}$=2且△ABP的面积为4,有以下结论:分析 设点A坐标为(m,$\frac{k}{m}$),点B坐标为(n,$\frac{k}{n}$),结合$\frac{AP}{PC}$=2且△ABP的面积为4列出关于m、n和k的分式方程组,解方程组得出m、n之间的关系以及k的值,由此得出②不成立;①由A、B点的坐标,结合m、n之间的关系利用矩形的面积公式即可得知结论成立;③由A、B点的坐标和m、n之间的关系,结合两点间的距离即可得知结论成立;④由A、B点的坐标,结合m、n之间的关系利用矩形的面积公式即可得出S四边形AEDP=S四边形BPCF=4,即④不成立,从而得出正确的结论是①③.
解答 解:设点A坐标为(m,$\frac{k}{m}$),点B坐标为(n,$\frac{k}{n}$)(0<m<n).
由已知得:$\left\{\begin{array}{l}{\frac{k}{m}-\frac{k}{n}=2\frac{k}{n}}\\{(n-m)(\frac{k}{m}-\frac{k}{n})=4×2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=6}\\{n=3m}\end{array}\right.$.
故②k=12,不成立;
①四边形DPCO的面积S=OC•PC=m•$\frac{k}{n}$=m•$\frac{6}{3m}$=2,
即①成立;
③BP=n-m=2m,DP=m,
故$\frac{BP}{DP}=\frac{2m}{m}$=2,③成立;
④S四边形AEDP=AP•DP=($\frac{6}{m}$-$\frac{6}{n}$)•m=4,
S四边形BPCF=BP•PC=(n-m)•$\frac{6}{n}$=4,
故S四边形AEDP=S四边形BPCF=4,④不成立.
故答案为:①③.
点评 本题考查了反比例函数系数k的几何意义、三角形的面积公式以及矩形的面积公式,解题的关键是:设出A、B两点的坐标结合已知条件得出关于m、n和k的分式方程组,得出m、n之间的关键求出k值.本题属于基础题,难度不大,解决该题型题目的方法是:先根据题意列出方程组,求出m、n之间的关系和k的值后,再去判断各结论的对错.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
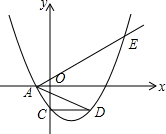 如图,抛物线y=$\frac{1}{{t}^{2}}$(x+t)(x-3t)交x轴负半轴于点A,交y轴于点C,点D,E均在抛物线上,且CD∥x轴,∠EAD=2∠ADC,求$\frac{AD}{AE}$的值.
如图,抛物线y=$\frac{1}{{t}^{2}}$(x+t)(x-3t)交x轴负半轴于点A,交y轴于点C,点D,E均在抛物线上,且CD∥x轴,∠EAD=2∠ADC,求$\frac{AD}{AE}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com