
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЕФСНИіЭМаЮMгыNЃЌИјГіШчЯТЖЈвхЃКPЮЊЭМаЮMЩЯШЮвтвЛЕуЃЌQЮЊЭМаЮNЩЯШЮвтвЛЕуЃЌШчЙћPЃЌQСНЕуМфЕФОрРыгазюаЁжЕЃЌФЧУДГЦетИізюаЁжЕЮЊЭМаЮMЃЌNМфЕФЁАКЭФРОрРыЁБЃЌМЧзїdЃЈMЃЌNЃЉЃЎШєЭМаЮMЃЌNгаЙЋЙВЕуЃЌдђdЃЈMЃЌNЃЉЃН0ЃЎ
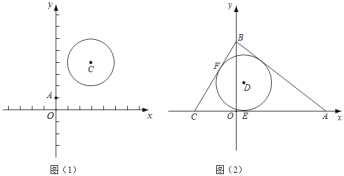
ЃЈ1ЃЉШчЭМЃЌAЃЈ0ЃЌ1ЃЉЃЌCЃЈ3ЃЌ4ЃЉЃЌЁбCЕФАыОЖЮЊ2ЃЌдђdЃЈCЃЌЁбCЃЉЃНЁЁ ЁЁЃЌdЃЈOЃЌЁбCЃЉЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉвбжЊЃЌШчЭМЃЌЁїABCЕФвЛБпACдкxжсЩЯЃЌBдкyжсЩЯЃЌЧвACЃН8ЃЌABЃН7ЃЌBCЃН5ЃЎ
ЂйDЪЧЁїABCФквЛЕуЃЌШєACЁЂBCЗжБ№ЧаЁбDгкEЁЂFЃЌЧвdЃЈCЃЌDЃЉЃН2dЃЈDЃЌABЃЉЃЌХаЖЯABгыЁбDЕФЮЛжУЙиЯЕЃЌВЂЧѓГіDЕуЕФзјБъЃЛ
ЂкШєвдrЮЊАыОЖЃЌЂйжаЕФDЮЊдВаФЕФЁбDЃЌгаdЃЈBЃЌЁбDЃЉЃО1ЃЌdЃЈCЃЌЁбDЃЉЃМ2ЃЌжБНгаДГіrЕФШЁжЕЗЖЮЇЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌ3ЃЛЃЈ2ЃЉЂйABЪЧЁбOЕФЧаЯпЃЌЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЭМаЮMЁЂMМфЕФЁАКЭФРОрРыЁБЕФЖЈвхМДПЩЧѓНт;
ЃЈ2ЃЉЂйСЌНгDFЃЌDEЃЌзїDHЁЭABгкH. ЩшOCЃНx.ЯШжЄУїЁЯCBOЃН30ЁуЃЌдйжЄУїDH=DEМДПЩНтОіЮЪЬт
ЂкЯШЧѓГіЕуDЕФзјБъЃЌСаГіВЛЕШЪНзщЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉЁпAЃЈ0ЃЌ1ЃЉЃЌCЃЈ3ЃЌ4ЃЉЃЌЁбCЕФАыОЖЮЊ2ЃЌ
ЁрdЃЈCЃЌЁбCЃЉЃН2ЃЌdЃЈOЃЌЁбCЃЉЃНOCЉ2ЃН![]() Љ2ЃН3ЃЌ
Љ2ЃН3ЃЌ
ЙЪД№АИЮЊ2ЃЌ3ЃЎ
ЃЈ2ЃЉЂйСЌНгDFЃЌDEЃЌзїDHЁЭABгкHЃЎЩшOCЃНxЃЎ
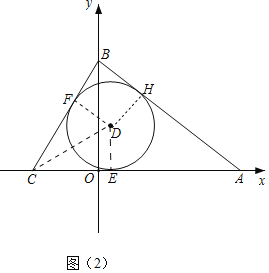
ЁпOB2ЃНBC2ЉOC2ЃНAB2ЉAO2ЃЌ
Ёр52Љx2ЃН72ЉЃЈ8ЉxЃЉ2ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрBCЃН2OCЃЌ
ЁрЁЯCBOЃН30ЁуЃЌЁЯBCOЃН60ЁуЃЌ
ЁпCEЃЌCFЪЧЁбOЕФЧаЯпЃЌ
ЁрCDЦНЗжЁЯBCAЃЌ
ЁрЁЯDCEЃНЁЯDCBЃН30ЁуЃЌ
ЁрDCЃН2DEЃЌ
ЁпdЃЈCЃЌDЃЉЃН2dЃЈDЃЌABЃЉЃЌ
ЁрCDЃН2DHЃЌ
ЁрDHЃНDEЃЌ
ЁрABЪЧЁбOЕФЧаЯпЃЎ
ЂкгЩЂйПЩжЊOBЃН![]() OCЃН
OCЃН![]() ЃЌЩшDFЃНDEЃНDHЃНxЃЌ
ЃЌЩшDFЃНDEЃНDHЃНxЃЌ
ЁпSЁїABCЃН![]() ACOCЃН
ACOCЃН![]() ЃЈAC+BC+ABЃЉxЃЌ
ЃЈAC+BC+ABЃЉxЃЌ
ЁрxЃН![]() ЃЌ
ЃЌ
ЁрCEЃН![]() DEЃН3ЃЌCDЃН2DEЃН2
DEЃН3ЃЌCDЃН2DEЃН2![]() ЃЌ
ЃЌ
ЁрOEЃН3Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЁпBЃЈ0ЃЌ
ЃЉЃЌЁпBЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрBDЃН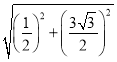 ЃН
ЃН![]() ЃЌ
ЃЌ
гЩЬтвтЃК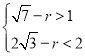 ЃЌ
ЃЌ
НтЕУ2![]() Љ2ЃМrЃМ
Љ2ЃМrЃМ![]() Љ1ЃЎ
Љ1ЃЎ
ЙЪД№АИЮЊ2![]() Љ2ЃМrЃМ
Љ2ЃМrЃМ![]() Љ1ЃЎ
Љ1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
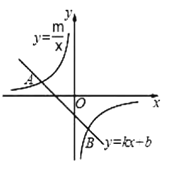
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЪЧвЛДЮКЏЪ§
ЪЧвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЕФСНИіНЛЕуЁЃ
ЕФЭМЯѓЕФСНИіНЛЕуЁЃ
ЃЈ1ЃЉЧѓДЫЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉИљОнЭМЯѓжБНгаДГіЪЙВЛЕШЪН![]() ГЩСЂЕФ
ГЩСЂЕФ![]() ЕФШЁжЕЗЖЮЇ______________________ЁЃ
ЕФШЁжЕЗЖЮЇ______________________ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЎдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЮЊAЃЈ-2ЃЌ1ЃЉЃЌBЃЈ-1ЃЌ4ЃЉЃЌCЃЈ-3ЃЌ2ЃЉЃЌ
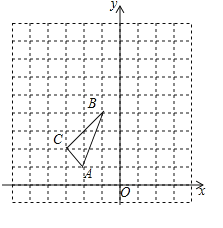
ЃЈ1ЃЉЛЁїABCЙигкyжсЖдГЦЕФЭМаЮЁїA1B1C1ЃЛ
ЃЈ2ЃЉвдOЮЊЮЛЫЦжааФЃЌдкЕкЖўЯѓЯоФкАбЁїABCРЉДѓЕНдРДЕФСНБЖЃЌЕУдђЁїA2B2C2ЃЌЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉЁїABCЕФУцЛ§ЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпcЃКy=x2+2xЉ3ЃЌНЋХзЮяЯпcЦНвЦЕУЕНХзЮяЯпcЁфЃЌШчЙћСНЬѕХзЮяЯпЃЌЙигкжБЯпx=1ЖдГЦЃЌФЧУДЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. НЋХзЮяЯпcбиxжсЯђгвЦНвЦ![]() ИіЕЅЮЛЕУЕНХзЮяЯпcЁф B. НЋХзЮяЯпcбиxжсЯђгвЦНвЦ4ИіЕЅЮЛЕУЕНХзЮяЯпcЁф
ИіЕЅЮЛЕУЕНХзЮяЯпcЁф B. НЋХзЮяЯпcбиxжсЯђгвЦНвЦ4ИіЕЅЮЛЕУЕНХзЮяЯпcЁф
C. НЋХзЮяЯпcбиxжсЯђгвЦНвЦ![]() ИіЕЅЮЛЕУЕНХзЮяЯпcЁф D. НЋХзЮяЯпcбиxжсЯђгвЦНвЦ6ИіЕЅЮЛЕУЕНХзЮяЯпcЁф
ИіЕЅЮЛЕУЕНХзЮяЯпcЁф D. НЋХзЮяЯпcбиxжсЯђгвЦНвЦ6ИіЕЅЮЛЕУЕНХзЮяЯпcЁф
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
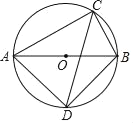
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌABЪЧЁбOжБОЖЃЌЁЯACBЕФЦНЗжЯпНЛЁбOгкDЃЌШєACЃНmЃЌBCЃНnЃЌдђCDЕФГЄЮЊ_____ЃЈгУКЌmЁЂnЕФДњЪ§ЪНБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќRtЁїABCжаЃЌBA=BCЃЌЁЯABC=90ЁуЃЌЕуDдкACЩЯЃЌНЋЁїABDШЦЕуBбиЫГЪБеыЗНЯђа§зЊ90ЁуКѓЃЌЕУЕНЁїCBEЃЎ
ЃЈ1ЃЉЧѓЁЯDCEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєAB=4ЃЌCD=3ADЃЌЧѓDEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвEFЁЭABгкЕуCЃЌЕуDЪЧABбгГЄЯпЩЯвЛЕуЃЌЁЯAЃН30ЁуЃЌЁЯDЃН30ЁуЃЎ
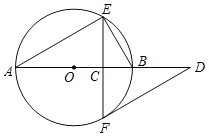
ЃЈ1ЃЉЧѓжЄЃКFDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШЁBEЕФжаЕуMЃЌСЌНгMFЃЌШєЁбOЕФАыОЖЮЊ2ЃЌЧѓMFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКХзЮяЯпyЃНaЃЈx+1ЃЉЃЈxЉ3ЃЉгыxжсЯрНЛгкAЁЂBСНЕуЃЌгыyжсЕФНЛгкЕуCЃЈ0ЃЌЉ3ЃЉЃЎ
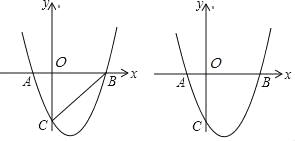
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЕФвЛАуЪНЃЎ
ЃЈ2ЃЉШєХзЮяЯпЩЯгавЛЕуPЃЌТњзуЁЯACOЃНЁЯPCBЃЌЧѓPЕузјБъЃЎ
ЃЈ3ЃЉжБЯпlЃКyЃНkxЉk+2гыХзЮяЯпНЛгкEЁЂFСНЕуЃЌЕБЕуBЕНжБЯпlЕФОрРызюДѓЪБЃЌЧѓЁїBEFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2+ЃЈ2m+1ЃЉx+mЃЈmЉ3ЃЉЃЌЃЈmЮЊГЃЪ§ЃЌЉ1ЁмmЁм4ЃЉЃЌAЃЈЉmЉ1ЃЌy1ЃЉЃЌ![]() ЪЧИУХзЮяЯпЩЯВЛЭЌЕФСНЕуЃЌЯжНЋХзЮяЯпЕФЖдГЦжсШЦзјБъдЕуOФцЪБеыа§зЊ90ЁуЕУЕНжБЯпaЃЌЙ§ХзЮяЯпЖЅЕуPзїPHЁЭaгкHЃЎ
ЪЧИУХзЮяЯпЩЯВЛЭЌЕФСНЕуЃЌЯжНЋХзЮяЯпЕФЖдГЦжсШЦзјБъдЕуOФцЪБеыа§зЊ90ЁуЕУЕНжБЯпaЃЌЙ§ХзЮяЯпЖЅЕуPзїPHЁЭaгкHЃЎ
ЃЈ1ЃЉЕБmЃН1ЪБЃЌЧѓГіетЬѕХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉШєЮоТлmШЁКЮжЕЃЌХзЮяЯпгыжБЯпyЃНxЉkmЃЈkЮЊГЃЪ§ЃЉгаЧвНігавЛИіЙЋЙВЕуЃЌЧѓkЕФжЕЃЛ
ЃЈ3ЃЉЕБ1ЃМPHЁм6ЪБЃЌЪдБШНЯy1ЃЌy2жЎМфЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com