
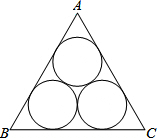
 如图,三个半径为
如图,三个半径为| 3 |
A、12+6
| ||
B、12+12
| ||
C、18+12
| ||
D、18+6
|
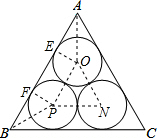 解:如图,∵连接AO、OP、PB、OE、PF、ON;
解:如图,∵连接AO、OP、PB、OE、PF、ON;| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
 随着生活质量的提高,人们的健康意识逐渐增强,安装静水设备的百姓家庭越来越多,某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示,今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
随着生活质量的提高,人们的健康意识逐渐增强,安装静水设备的百姓家庭越来越多,某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示,今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.查看答案和解析>>
科目:初中数学 来源: 题型:
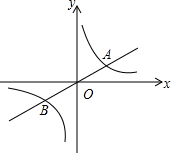 如图,已知直线y=
如图,已知直线y=| 1 |
| 2 |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或是3的倍数的概率等于( )
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或是3的倍数的概率等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com