
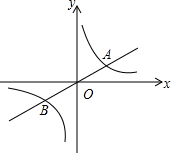
 如图,已知直线y=
如图,已知直线y=| 1 |
| 2 |
| k |
| x |
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| 8 |
| x |
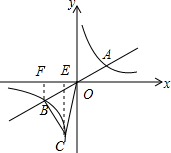
| 8 |
| x |
| 1 |
| 2 |
| k |
| x |


科目:初中数学 来源: 题型:
|
| A、0或2个 |
| B、0或1或2个 |
| C、0或2或4个 |
| D、0或2或3或4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
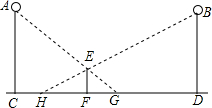 如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是
如图,晚上,身高1.5米的小颖站在两盏相距25米的同样高的路灯之间.现测得她在路灯A照射下的影长FG为2米,她在路灯B照射下的影长FH为3米,则这两盏路灯的高度是查看答案和解析>>
科目:初中数学 来源: 题型:
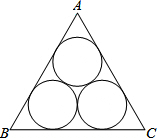 如图,三个半径为
如图,三个半径为| 3 |
A、12+6
| ||
B、12+12
| ||
C、18+12
| ||
D、18+6
|
查看答案和解析>>
科目:初中数学 来源: 题型:
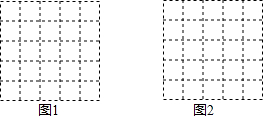 所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形,在一个由5×5个边长为1的小正方形组成的正方形格点中.画出符合要求的格点三角形.
所谓格点三角形指的是三角形的三个顶点均在正方形的格点上的三角形,在一个由5×5个边长为1的小正方形组成的正方形格点中.画出符合要求的格点三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点P是∠BAC的平分线AD上的一点,PE⊥AC于点E,PE=3,若点F是AB边上的一个动点,则PF的最小值等于( )
如图,点P是∠BAC的平分线AD上的一点,PE⊥AC于点E,PE=3,若点F是AB边上的一个动点,则PF的最小值等于( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com