
����Ŀ����12�֣���ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�
��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�![]() ����P��ֱ��BC�·��������ϵ�һ�����㣮
����P��ֱ��BC�·��������ϵ�һ�����㣮
��1������κ�������ʽ��
��2������PO��PC��������POC��y����ۣ��õ��ı���![]() .�Ƿ���ڵ�P��ʹ�ı���
.�Ƿ���ڵ�P��ʹ�ı���![]() Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC��������.


���𰸡���1��![]() ��2��
��2��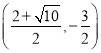 ��3��
��3��![]() ��
�� ![]() .
.
�������������������1�����ô���ϵ��������B��C��������������ߵĽ���ʽ�м�����ô���ϵ����ֵ������Ϳɵý⣻
��2����PE��CO��E���������εĶԽ����ഹֱƽ�֣����ı���POP��CΪ���Σ���ôP�����OC�Ĵ�ֱƽ�����ϣ��ݴˣ������ֱ��PE�Ľ���ʽ�����������ߵĽ���ʽ���������P������ꣻ
��3��������ABC�����Ϊ��ֵ�����ı���ABPC��������ʱ����BPC��������P��y���ƽ���ߣ���ֱ��BC��Q����x����F�������ֱ��BC�Ľ���ʽ�������P��ĺ����꣬Ȼ����������ߺ�ֱ��BC�Ľ���ʽ���Q��P�������꣬���ɵõ�PQ�ij�����PQΪ�ף�B�������ľ���ֵΪ���������BPC��������ɴˣ��ɵõ������ı���ACPB�������P�������ĺ�����ϵʽ���ٸ��ݺ��������ʼ�������ı���ABPC������������Ӧ��P������.
�����������1����B��C������������![]() ����
����![]()
��֮����![]()
���Զ��κ����Ľ���ʽΪ![]() .
.
��2����ͼ1�������������ϴ��ڵ�P��ʹ�ı���![]() Ϊ���Σ�����
Ϊ���Σ�����![]() ��CO�ڵ�E��
��CO�ڵ�E��
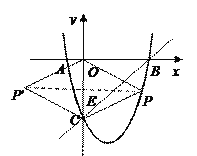
���ı���![]() Ϊ���Σ�
����
��PC=PO����PE��CO��
��OE=EC=![]() ����P���������Ϊ
����P���������Ϊ![]()
��![]() =
=![]() ����
����
![]() ���������⣬��ȥ��
���������⣬��ȥ��
���Դ��������ĵ㣬��ʱP�������Ϊ��![]() ��
�� ![]() ��.
��.
��3����ͼ2������PO����PM��x��M��PN��y��N����P������Ϊ��x�� ![]() ����
����

��![]() =0���õ�A����Ϊ����1��0��.
=0���õ�A����Ϊ����1��0��.
��AO=1��OC=3�� OB=3��P��=![]() ��PN��x��
��PN��x��
��S�ı���ABPC=![]() +
+![]() +
+![]()
=![]() AO��OC+
AO��OC+![]() OB��PM+
OB��PM+![]() OC��PN
OC��PN
=![]() ��1��3+
��1��3+![]() ��3��(
��3��(![]() )+
)+![]() ��3��x
��3��x
=![]()
=![]() .
.
��֪����x=![]() ʱ���ı���ABPC��������ʱP������Ϊ��
ʱ���ı���ABPC��������ʱP������Ϊ��![]() ��
�� ![]() �����ı���ABPC��������Ϊ
�����ı���ABPC��������Ϊ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2��bx��c��ͼ����x�ύ��A��B���������е�A(��1��0)����C(0��5)����D(1��8)����������������֪MΪ�����ߵĶ�����

(1)�������ߵı���ʽ��
(2)���MCB�������
(3)����ͼ��ֱ��д��ʹֱ��MC��ʾ��һ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��PM2.5�Ǵ�����ֱ��С�ڻ����0.0000025m�Ŀ����PM2.5����С���������ǿ�������ж����к����ʣ����磬�ؽ���������ȣ������ڴ����е�ͣ��ʱ�䳤�����;���Զ����������彡���ʹ������������нϴ��Ӱ�죮�����ォ����0.0000025�ÿ�ѧ��������ʾΪ�� ��
A. 0.25��10��5B. 0.25��10��6C. 2.5��10��5D. 2.5��10��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
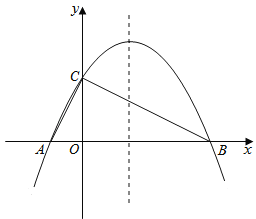
����Ŀ����ͼ����֪������y=��![]() x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
��1���������ߵĽ���ʽ�����ĶԳ��
��2�����C�����꣬����AC��BC�����߶�BC����ֱ�ߵĽ���ʽ��
��3���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������ߣ�y=��x��x��3����0��x��3������ΪC1������x�ύ�ڵ�O��A1��
��C1�Ƶ�A1��ת180����C2����x���ڵ�A2��
��C2�Ƶ�A2��ת180����C3����x���ڵ�A3��
��
��˽�����ȥ��ֱ����C13����P��37��m���ڵ�13��������C13�ϣ���m=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���֪������y1=ax2+bx+c��a��0����x���ཻ�ڵ�A��B����A��B��ԭ��O���ࣩ����y���ཻ�ڵ�C���ҵ�A��C��һ�κ���y2=![]() x+n��ͼ���ϣ��߶�AB��Ϊ16���߶�OC��Ϊ8����y1����x���������Сʱ�����Ա���x��ȡֵ��Χ��
x+n��ͼ���ϣ��߶�AB��Ϊ16���߶�OC��Ϊ8����y1����x���������Сʱ�����Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣��ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ��������������Ϣ���±���

��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ��
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ı���ABCD�У���A����B����C����D�Ķ���֮�ȣ��������ж��ı���ABCDΪƽ���ı��ε���( )
A. 1��2��3��4 B. 2��3��2��3
C. 2��2��3��3 D. 1��2��2��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com