
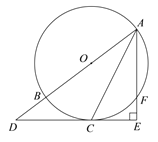
【题目】如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若AE=3,DE=4,求⊙O的半径的长.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
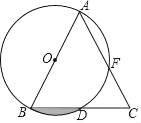
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连结AB.
(1)求证:AB2=AE·AD;
(2)若AE=2,ED=4,求图中阴影的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
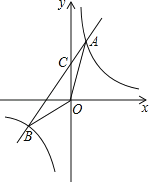
【题目】如图,已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
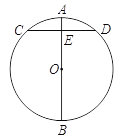
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班的各5名学生的成绩,它们分别为:
九(1)班 :96,92,94,97,96;
九(2)班 :90,98,97,98,92.
通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 |
九(1)班 | 95 | a | 96 |
九(2)班 | 95 | 97 | b |
(1)a= , b = ;
(2)计算两个班所抽取的学生艺术成绩的方差,判断哪个班学生的艺术成绩比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )

A.①③④ B.①②③ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到________m/s.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com