
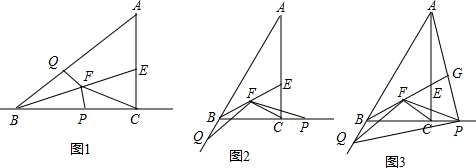
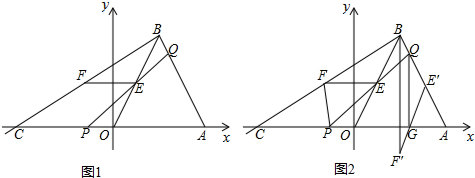
分析 (1)如图1,根据直角三角形斜边上的中线性质得到FB=FC=FE,再根据等腰三角形的性质得到相应的角相等,于是可证明△BFQ≌△CFP,得到BQ=CP,所以BQ+BP=PC+BP=BC,然后根据三角函数的定义得到tan∠ABC=$\frac{AC}{BC}$=$\frac{3}{4}$,即BC=$\frac{4}{3}$AC,于是得到BQ+BP=$\frac{4}{3}$AC;
(2)如图2,先证明△BFQ≌△CFP得到BQ=CP,则BC=BQ-BP,再利用三角函数的定义得∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,则BC=$\frac{3}{4}$AC,所以BQ-BP=$\frac{3}{4}$AC;
((3)作QH⊥BC于H,作GN∥BC交AC于N,如图3,先计算出BC=3,AC=4,PQ=3$\sqrt{2}$,再利用角平分线定理得到$\frac{CE}{AE}$=$\frac{BC}{BA}$=$\frac{3}{5}$,则可计算出CE=$\frac{3}{8}$AC=$\frac{3}{2}$,接着利用勾股定理计算出BE=$\frac{3\sqrt{5}}{2}$;由于∠ABC=∠HBQ,则在Rt△BHQ中,tan∠HBQ=$\frac{HQ}{BH}$=$\frac{4}{3}$,设HQ=4x,BH=3x,则BQ=5x,PC=BQ=5x,在Rt△PHQ中根据勾股定理得到(4x)2+(8x+3)2=(3$\sqrt{2}$)2,得x1=$\frac{3}{20}$,x2=-$\frac{3}{4}$(舍去),所以PC=5x=$\frac{3}{4}$,BP=$\frac{15}{4}$,再利用角平分线定理得到$\frac{AG}{PG}$=$\frac{BA}{BP}$=$\frac{4}{3}$,由比例性质得$\frac{AG}{AP}$=$\frac{4}{7}$,然后证明△ANG∽△ACP,利用相似比计算出NG=$\frac{3}{7}$,接着证明△ENG∽△ECB,于是利用相似比可计算出EG=$\frac{3\sqrt{5}}{14}$.
解答 (1)证明:如图1,
∵BE平分∠ABC,
∴∠1=∠3,
∵F点为BE的中点,
∴FB=FC=FE,
∴∠1=∠2,
∴∠3=∠2,
在△BFQ和△CFP中
$\left\{\begin{array}{l}{∠3=∠2}\\{BF=CF}\\{∠BFQ=∠PFC}\end{array}\right.$,
∴△BFQ≌△CFP,
∴BQ=CP,
∴BQ+BP=PC+BP=BC,
在Rt△ABC中,∵tan∠ABC=$\frac{AC}{BC}$=$\frac{3}{4}$,
∴BC=$\frac{4}{3}$AC,
∴BQ+BP=$\frac{4}{3}$AC;
(2)解:BQ-BP=$\frac{3}{4}$AC.理由如下: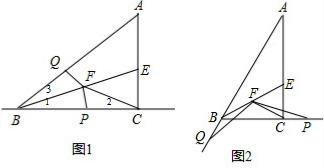
如图2,∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵F点为BE的中点,
∴FB=FC=FE,
∴∠CBE=∠FCB,
∴∠ABE=∠FCB,
∴∠FBQ=∠FCP,
在△BFQ和△CFP中
$\left\{\begin{array}{l}{∠BFQ=∠CFP}\\{BF=CF}\\{∠FBQ=∠FCP}\end{array}\right.$,
∴△BFQ≌△CFP,
∴BQ=CP,
∴BC=BQ-BP,
在Rt△ABC中,∵tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,
∴BC=$\frac{3}{4}$AC,
∴BQ-BP=$\frac{3}{4}$AC;
故答案为BQ-BP=$\frac{3}{4}$AC;
(3)解:作QH⊥BC于H,作GN∥BC交AC于N,如图3,
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,
而AB=5,
∴BC=3,AC=4,
∴PQ=3$\sqrt{2}$,
∵BE平分∠ABC,
∴$\frac{CE}{AE}$=$\frac{BC}{BA}$=$\frac{3}{5}$,
∴$\frac{CE}{CA}$=$\frac{3}{8}$,
∴CE=$\frac{3}{8}$AC=$\frac{3}{2}$,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,
∵∠ABC=∠HBQ,
∴tan∠HBQ=$\frac{3}{4}$,
在Rt△BHQ中,tan∠HBQ=$\frac{HQ}{BH}$=$\frac{4}{3}$,
设HQ=4x,BH=3x,则BQ=5x,
∴PC=BQ=5x,
∴PH=3x+3+5x=8x+3,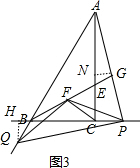
在Rt△PHQ中,∵QH2+PH2=PQ2,
∴(4x)2+(8x+3)2=(3$\sqrt{2}$)2,
整理得80x2+48x-9=0,解得x1=$\frac{3}{20}$,x2=-$\frac{3}{4}$(舍去),
∴PC=5x=$\frac{3}{4}$,
∴BP=3+$\frac{3}{4}$=$\frac{15}{4}$,
∴BG平分∠ABP,
∴$\frac{AG}{PG}$=$\frac{BA}{BP}$=$\frac{5}{\frac{15}{4}}$=$\frac{4}{3}$
∴$\frac{AG}{AP}$=$\frac{4}{7}$,
∵GN∥PC,
∴△ANG∽△ACP,
∴$\frac{NG}{CP}$=$\frac{AG}{AP}$=$\frac{4}{7}$,
∴NG=$\frac{4}{7}$×$\frac{3}{4}$=$\frac{3}{7}$,
∵NG∥BC,
∴△ENG∽△ECB,
∴$\frac{EG}{BE}$=$\frac{NG}{BC}$,即$\frac{EG}{\frac{3\sqrt{5}}{2}}$=$\frac{\frac{3}{7}}{3}$,
∴EG=$\frac{3\sqrt{5}}{14}$.
点评 本题考查了相似形综合题:熟练掌握相似三角形的判断与性质、全等三角形的判定与性质,会利用勾股定理和锐角三角函数的定义计算相应线段的长.本题的关键是作辅助线构造直角三角形和相似三角形.


科目:初中数学 来源: 题型:选择题
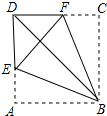 如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )
如图,将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为( )| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知在Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为$\frac{1}{{2}^{2012}}$.
如图,已知在Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为$\frac{1}{{2}^{2012}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
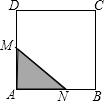 如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )
如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )| A. | 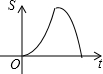 | B. | 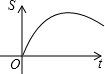 | C. | 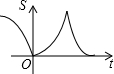 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com