
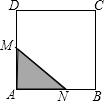
 如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )
如图,在边长为4cm的正方形ABCD中,点M、N同时从点A出发,均以1cm/s的速度沿折线ADC与折线ABC运动至C.设△AMN的面积为Scm2,运动时间为ts,则S关于t的函数图象大致为( )| A. | 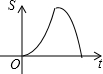 | B. | 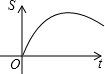 | C. | 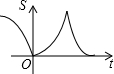 | D. | 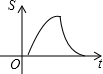 |
分析 根据题中条件可知在运动过程△AMN有两种不同情形,分别求出△AMN的面积Scm2与运动时间为ts的函数解析式为:$S△=\frac{1}{2}{t^2}\;\;\;(0<t≤4)$或$S△=-\frac{1}{2}{t^2}+4t\;\;\;(4<t<8)$,即可解答.
解答 解:如图,可知在运动过程△AMN有两种不同情形,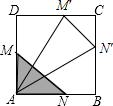
当0<t≤4时,即当点M在AD边,点N在AB边上运动时,AM=AN=t,
∴${S}_{AMN}=\frac{1}{2}•t•t=\frac{1}{2}{t}^{2}$,
当4<t<8时,即当点M在CD边,点N在BC边上运动时,DM′=BN′=t-4,CM′=CN′=4-(t-4)=8-t,
∴S△AMN=${4}^{2}-\frac{1}{2}×4(t-4)-\frac{1}{2}×4(t-4)-\frac{1}{2}(8-t)^{2}$=$-\frac{1}{2}{t}^{2}+4t$,
∴△AMN的面积Scm2与运动时间为ts的函数解析式为:$S△=\frac{1}{2}{t^2}\;\;\;(0<t≤4)$或$S△=-\frac{1}{2}{t^2}+4t\;\;\;(4<t<8)$,
故选:A.
点评 本题考查动点问题的函数图象,解决本题的关键是求出在不同时间段的函数解析式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 甲印刷社 | 0.15元/张 | |
| 乙印刷社 | 500张以内(含500张) | 0.20元/张 |
| 超过500张部分 | 0.10元/张 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
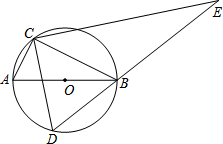 如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.
如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
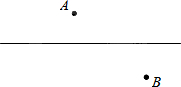 如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求在图中画图,并把答案填写在横线上.
按要求在图中画图,并把答案填写在横线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
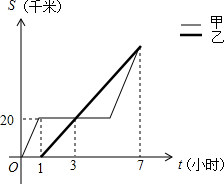 甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:
甲、乙两人骑自行车分别从A地出发,沿同一路线去B地,甲先行1小时到达距离A地20千米的C地,甲因事耽误一会儿,事后继续按原速行驶,并与乙同时到达B地,如图表示甲、乙两人骑自行车行驶的路程S(千米)岁时间t(小时)变化图象(全程),据图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com