
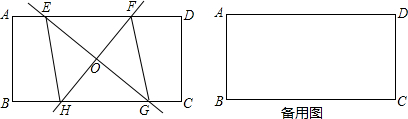
分析 (1)四边形EFGH是菱形,先由矩形ABCD是中心对称图形,O是对称中心,可得OE=OG,OF=OH,进而可证四边形EFGH是平行四边形,然后由EG⊥FH,根据对角线互相垂直的平行四边形是菱形,即可判断平行四边形EFGH是菱形;
(2)分3种情况讨论:①当F在边AD上时,即0≤x≤$\frac{3}{2}$,作OM⊥AD于M,如图1,然后表示出OM=1,EM=2-x,然后证明△EMO∽△OMF,进而由相似三角形的对应边成比例,可得$\frac{MF}{OM}=\frac{OM}{EM}$,进而表示出FM=$\frac{1}{2-x}$,EF=2-x+$\frac{1}{2-x}$,最后利用菱形的面积公式计算即可;②当F在边CD上时,即$\frac{3}{2}$<x≤$\frac{5}{2}$,作OM⊥AD于M,作OM⊥CD于N,如图2,然后同①表示OM=1,ON=2,EM=x-2,然后证明△OME∽△ONF,进而由相似三角形的对应边成比例,可得$\frac{OF}{OE}=\frac{ON}{OM}$=2,进而表示出:OF=2OE,然后在Rt△OME中,由勾股定理表示出OE2=1+(x-2)2,最后利用菱形的面积公式计算即可;③当F在边BC上时,即$\frac{5}{2}<x≤4$,作OM⊥AD于M,如图3,然后表示OM=1,EM=x-2,然后证明△EMO∽△OMH,进而由相似三角形的对应边成比例,可得$\frac{EM}{OM}=\frac{OM}{MH}$,进而表示出:MH=$\frac{1}{x-2}$,进而表示EH=x-2+$\frac{1}{x-2}$,最后利用菱形的面积公式计算即可;
(3)在矩形ABCD中,AB=2,AD=4,可得矩形的面积为2×4=8,然后分别令(2)中S=4,即可求出x的值.
解答 解:(1)四边形EFGH是菱形,
理由:∵矩形ABCD是中心对称图形,O是对称中心,
∴OE=OG,OF=OH∴四边形EFGH是平行四边形,
∵EG⊥FH,
∴平行四边形EFGH是菱形; 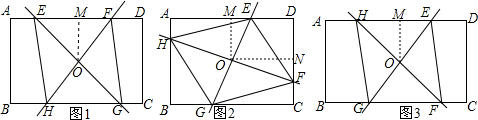 (2)①当F在边AD上时,作OM⊥AD于M,如图1,
(2)①当F在边AD上时,作OM⊥AD于M,如图1,
则OM=1,EM=2-x,
∵∠EOF=90°,
∴∠OEM+∠OFM=90°,
∵OM⊥AD,
∴∠EMO=∠FMO=90°,
∴∠OEM+∠EOM=90°,
∴∠OFM=∠EOM,
在Rt△EMO和Rt△OMF中,
$\left\{\begin{array}{l}{∠OFM=∠EOM}\\{∠EMO=∠FMO}\end{array}\right.$,
∴△EMO∽△OMF,
∴$\frac{MF}{OM}=\frac{OM}{EM}$,
即$\frac{FM}{1}=\frac{1}{2-x}$,
∴FM=$\frac{1}{2-x}$,
∴EF=EM+FM=2-x+$\frac{1}{2-x}$,
∴S=2(2-x+$\frac{1}{2-x}$)=4-2x+$\frac{2}{2-x}$,(0$≤x≤\frac{3}{2}$);
②当F在边CD上时,作OM⊥AD于M,作OM⊥CD于N,如图2,
则OM=1,ON=2,EM=x-2,
∵OM⊥AD于M,作OM⊥CD于N,∠D=90°,
∴四边形MOND是矩形,
∴∠MON=90°,
∴∠MOE+∠EON=90°,
∵∠EOF=90°,
∴∠EON+∠FON=90°,
∴∠MOE=∠FON,
在△OME和△ONF中,
$\left\{\begin{array}{l}{∠OME=∠ONF}\\{∠MOE=∠NOF}\end{array}\right.$,
∴△OME∽△ONF,
∴$\frac{OF}{OE}=\frac{ON}{OM}$,
即$\frac{OF}{OE}=\frac{2}{1}=2$,
∴OF=2OE,
在Rt△OEM中,由勾股定理得:
OE2=OM2+ME2=1+(x-2)2,
∴S=$\frac{1}{2}$EG•EF=2•OE•OF=4•OE2=4[1+(x-2)2]=4(x-2)2+4,($\frac{3}{2}<x≤\frac{5}{2}$);
③当F在边BC上时,作OM⊥AD于M,如图3,
则OM=1,EM=x-2,
∵OM⊥AD,
∴∠HMO=∠EMO=90°,
∴∠MHO+∠MOH=90°,
∵∠HOE=90°,
∴∠MOH+∠MOE=90°,
∴∠MHO=∠MOE,
在△EMO和△OMH中,
$\left\{\begin{array}{l}{∠MHO=∠MOE}\\{∠HMO=∠EMO}\end{array}\right.$,
∴△EMO∽△OMH,
∴$\frac{EM}{OM}=\frac{OM}{MH}$,
即:$\frac{x-2}{1}=\frac{1}{MH}$,
∴MH=$\frac{1}{x-2}$,
∴EH=MH+ME=x-2+$\frac{1}{x-2}$,
∴S=2(x-2+$\frac{1}{x-2}$)=2x-4+$\frac{2}{x-2}$,($\frac{5}{2}<x≤4$);
∴用含x的代数式表示S为:$\left\{\begin{array}{l}{S=4-2x+\frac{2}{2-x}(0≤x≤\frac{3}{2})}\\{S=4(x-2)^{2}+4(\frac{3}{2}<x≤\frac{5}{2})}\\{S=2x-4+\frac{2}{x-2}(\frac{5}{2}<x≤4)}\end{array}\right.$;
(3)∵在矩形ABCD中,AB=2,AD=4,
∴S矩形ABCD=2×4=8,
∵S等于矩形面积的一半,
∴S=8×$\frac{1}{2}$=4,
①当0$≤x≤\frac{3}{2}$时,由4-2x+$\frac{2}{2-x}$=4,
解得:x=1,
②当$\frac{3}{2}<x≤\frac{5}{2}$时,由4(x-2)2+4=4,
解得:x=2,
③当$\frac{5}{2}<x≤4$时,由2x-4+$\frac{2}{x-2}$=4,
解得:x=3,
综上所述:x的值为1或2或3.
点评 此题是四边形的综合题,涉及的知识点有:矩形的性质,菱形的判定和菱形的面积公式,相似三角形的判定与性质,勾股定理等知识,解题的关键是:问题(2)要分3种情况讨论:①当F在边AD上时,②当F在边CD上时,③当F在边BC上时.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:选择题
| A. | (x+y)2=49 | B. | x2+y2=65 | C. | (x-y)2=81 | D. | (xy)2=-64 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$-$\sqrt{3}$ | C. | -$\sqrt{2}$-$\sqrt{3}$ | D. | $\sqrt{3}$-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
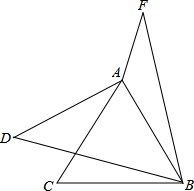 如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.
如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com