
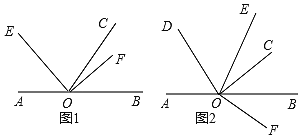
【题目】已知点O为直线AB上的一点,∠EOF为直角,OC平分∠BOE.
(1)如图1,若∠AOE=45°,写出∠COF等于多少度;
(2)如图1,若∠AOE=![]() 求∠COF的度效(用含
求∠COF的度效(用含![]() 的代数式表示);
的代数式表示);
(3)如图2,若∠AOE=![]() OD平分∠AOC,且∠AOD-∠BOF=45°,求
OD平分∠AOC,且∠AOD-∠BOF=45°,求![]() 的值。
的值。
【答案】(1)22.5° (2)![]() n° (3) 120
n° (3) 120
【解析】
(1)由∠AOE=45°,可以求得∠BOE=135°,再由OC平分∠BOE,可求得∠COE=67.5°,∠EOF为直角,所以可得∠COF=∠EOF-∠EOC=22.5°;
(2)由(1)的方法即可得到∠COF=![]() n°;
n°;
(3)先设∠BOF为x°,再根据角的关系得出方程,解答后求出n的值即可.
解:(1)∵∠AOE=45°,
∴∠BOE=135°,
∵OC平分∠BOE,
∴∠COE=67.5°,
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=22.5°,
(2))∵∠AOE=n°,
∴∠BOE=180°-n°,
∵OC平分∠BOE,
∴∠COE=![]() (180°-n°),
(180°-n°),
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=90°-![]() (180°-n°)=
(180°-n°)=![]() n°,
n°,
(3)设∠BOF为x°,∠AOD为(x+45)°,∠EOB为(90-x)°,OC平分∠BOE,
则可得:∠AOD+∠DOC+∠EOB=∠AOB+∠EOC.
x+45+x+45+90-x=180+![]() (90-x),
(90-x),
解得:x=30,
所以可得:∠EOB=(90-x)°=60°,
∠AOE=180°-∠EOB=180°-60°=120°,
故n的值是120.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别沿同一条路线从
,甲、乙两车分别沿同一条路线从![]() 地出发驶往
地出发驶往![]() 地,已知甲车的速度为
地,已知甲车的速度为![]() ,乙车的速度为
,乙车的速度为![]() ,甲车先出发
,甲车先出发![]() 后乙车再出发,乙车到达
后乙车再出发,乙车到达![]() 地后再原地等甲车.
地后再原地等甲车.
(1)求乙车出发多长时间追上甲车?
(2)求乙车出发多长时间与甲车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
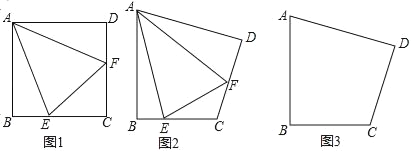
【题目】已知在四边形ABCD中,点E、F分别是BC、CD边上的一点.
(1)如图1:当四边形ABCD是正方形时,且∠EAF=45°,则EF、BE、DF满足的数量关系是 ,请说明理由;
(2)如图2:当AB=AD,∠B=∠D=90°,∠EAF是∠BAD的一半,问:(1)中的数量关系是否还存在? (填是或否)
(3)在(2)的条件下,将点E平移到BC的延长线上,请在图3中补全图形,并写出EF、BE、DF的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B , C重合),过M作MN∥ ![]() 轴交抛物线于N , 若点M的横坐标为
轴交抛物线于N , 若点M的横坐标为 ![]() ,请用含
,请用含 ![]() 的代数式表示线段MN的长。
的代数式表示线段MN的长。
(4)在(3)的条件下,连接NB、NC , 则是否存在点M,使△BNC的面积最大?若存在,求 ![]() 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1 , 0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )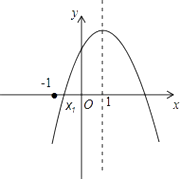
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a(a-3)-(-a+![]() )(-a-
)(-a-![]() );
);
(2)(2x-y)(y+2x)-4(y-x)(-x-y);
(3)(3a+1)(9a2+1)(3a-1);
(4)(1-x)(1+x2)(1+x)(1+x4).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG. 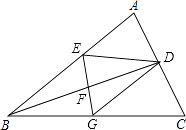
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com