
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG. 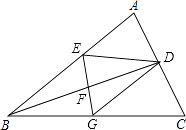
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长.
【答案】
(1)解:四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
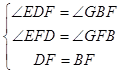 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形
(2)解:作DH⊥BC于H,
∵四边形EBGD为菱形ED=DG=2,
∴∠ABC=30°,∠DGH=30°,
∴DH=1,GH= ![]() ,
,
∵∠C=45°,
∴DH=CH=1,
∴CG=GH+CH=1+ ![]() .
.
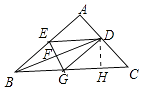
【解析】(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.(2)作DH⊥BC于H,由四边形EBGD为菱形ED=DG=2,求出GH,CH即可解决问题.
【考点精析】通过灵活运用线段垂直平分线的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
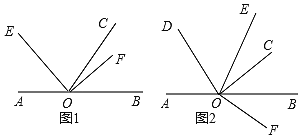
【题目】已知点O为直线AB上的一点,∠EOF为直角,OC平分∠BOE.
(1)如图1,若∠AOE=45°,写出∠COF等于多少度;
(2)如图1,若∠AOE=![]() 求∠COF的度效(用含
求∠COF的度效(用含![]() 的代数式表示);
的代数式表示);
(3)如图2,若∠AOE=![]() OD平分∠AOC,且∠AOD-∠BOF=45°,求
OD平分∠AOC,且∠AOD-∠BOF=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A. (-m +n)(m - n) B. (![]() a +b)(b -
a +b)(b -![]() a)
a)
C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
查看答案和解析>>
科目:初中数学 来源: 题型:
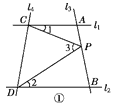
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
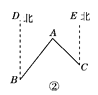
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
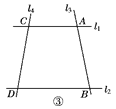
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E. 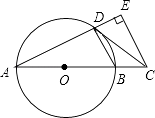
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
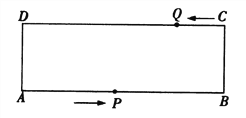
【题目】如图,在矩形ABCD中,AB=24 cm, BC=8 cm,点P从点A开始沿折线A-B-C-D以4 cm/s的速度移动,点Q从点C开始沿CD边以2 cm/s的速度移动,如果点P,Q分别从点A,C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为ts.当t为何值时,四边形QPBC为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(﹣4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO. 
(1)求BC的长;
(2)求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com