
【题目】如图: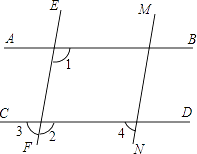
(1)已知AB∥CD,EF∥MN,∠1=115°,求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.
【答案】
(1)
解:∵AB∥CD,∠1=115°,
∴∠2=∠1=115°,
∵EF∥MN,
∴∠4=180°﹣∠2=180°﹣115°=65°
(2)
解:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补
(3)
解:根据(2)设其中一个角为x,则另一个角为2x,
则x+2x=180°,
解得x=60°,
故这两个角的大小为60°,120°
【解析】(1)∠1与∠2是平行线AB、CD被EF所截的同位角,∠2与∠4是平行线EF、MN被CD所截的同旁内角,根据两直线平行,内错角相等、同旁内角互补解答即可;(2)从∠2和∠4的边与∠1的两边互相平行和角的数量关系考虑;(3)设出两角,根据两角互补的关系列方程求解即可.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.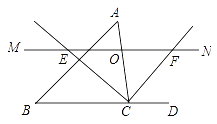
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论;
(3)在(2)的条件下,试猜想当△ABC满足什么条件时使四边形AECF是正方形,请直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( ) 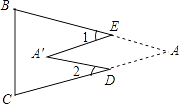
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE. 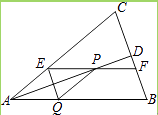
(1)求证:四边形AEPQ为菱形;
(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为解决大班额问题,对学校进行扩建,计划用三年时间对全县学校进行扩建和改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为( )
A. 20%、﹣220%B. 40%C. ﹣220%D. 20%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com