
【题目】如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE. 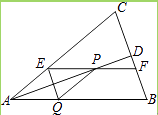
(1)求证:四边形AEPQ为菱形;
(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?
【答案】
(1)证明:∵EF∥AB,PQ∥AC,
∴四边形AEPQ为平行四边形,
∴∠BAD=∠EPA,
∵AB=AC,AD平分∠CAB,
∴∠CAD=∠BAD,
∴∠CAD=∠EPA,
∴EA=EP,
∴四边形AEPQ为菱形.
(2)解:P为EF中点时,S菱形AEPQ= ![]() S四边形EFBQ
S四边形EFBQ
∵四边形AEPQ为菱形,
∴AD⊥EQ,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴EQ∥BC,
又∵EF∥AB,
∴四边形EFBQ为平行四边形.
作EN⊥AB于N,如图所示:
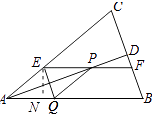
则S菱形AEPQ=EPEN= ![]() EFEN=
EFEN= ![]() S四边形EFBQ.
S四边形EFBQ.
【解析】(1)先证出四边形AEPQ为平行四边形,关键是找一组邻边相等,由AD平分∠BAC和PE∥AQ可证∠EAP=∠EPA,得出AE=EP,即可得出结论;(2)S菱形AEPQ=EPh,S平行四边形EFBQ=EFh,若菱形AEPQ的面积为四边形EFBQ面积的一半,则EP= ![]() EF,因此P为EF中点时,S菱形AEPQ=
EF,因此P为EF中点时,S菱形AEPQ= ![]() S四边形EFBQ .
S四边形EFBQ .


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数y=kx-1(k≠0)在第一象限的图象交于A(1,n)和B两点.
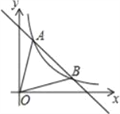
(1)求反比例函数的解析式与点B坐标;
(2)求△AOB的面积;
(3)在第一象限内,当一次函数y=﹣x+5的值小于反比例函数y=kx-1(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).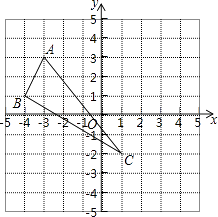
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′( , ); B′( , );
C′( , ).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图: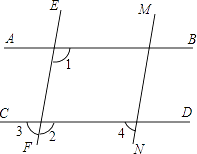
(1)已知AB∥CD,EF∥MN,∠1=115°,求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
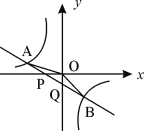
【题目】 (2016湖北鄂州第14题)如图,已知直线 ![]() 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y=![]() 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+![]() n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b>![]() 的解集是x<-2或0<x<1,其中正确的结论的序号是 .
的解集是x<-2或0<x<1,其中正确的结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整. 解:∵AD∥CB( 已知 )
∴∠C+∠ADC=180° ()
又∵∠A=∠C ()
∴∠A+∠ADC=180° ()
∴AB∥CD ()
∴∠BDC=∠ABD=32° ().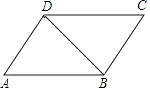
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com