
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠ACB的外角平分线CF于点F,交∠ACB内角平分线CE于E.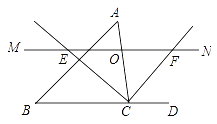
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论;
(3)在(2)的条件下,试猜想当△ABC满足什么条件时使四边形AECF是正方形,请直接写出你的结论.
【答案】
(1)
证明:如图1中,
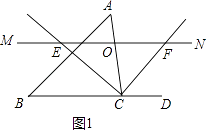
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF.
(2)
结论:当点O运动到AC中点处时,四边形AECF是矩形.
理由:如图2中,
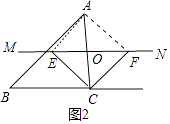
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE= ![]() ∠ACB,
∠ACB,
同理,∠ACF= ![]() ∠ACG,
∠ACG,
∴∠ECF=∠ACE+∠ACF= ![]() (∠ACB+∠ACG)=
(∠ACB+∠ACG)= ![]() ×180°=90°,
×180°=90°,
∴四边形AECF是矩形.:
(3)
解:结论:当∠ACB=90°时,四边形AECF是正方形
理由:∵∠BCA=90°,
∵MN∥BC,
∴∠BCA=∠AOM=90°,
∴AC⊥EF,
∴四边形AECF是正方形..
【解析】(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的判定方法解答.
【考点精析】解答此题的关键在于理解正方形的判定方法的相关知识,掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=4cm,BC=3cm,CD=12cm,DA=13cm,且∠ABC=90°,则四边形ABCD的面积为( ) 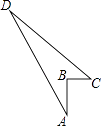
A.6cm2
B.30cm2
C.24cm2
D.36cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.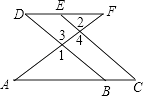
解:∵∠1=∠2(已知),
∠1=∠3(),
∴∠2=∠3(等量代换).
∴∥(同位角相等,两直线平行).
∴∠C=∠ABD ().
又∵∠C=∠D(已知),
∴∠D=∠ABD(等量代换).
∴AC∥DF().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
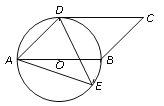
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图: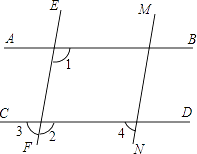
(1)已知AB∥CD,EF∥MN,∠1=115°,求∠2和∠4的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,试着用文字表述出来;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com