
【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从
A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.

(1)用含t的代数式表示P到点A和点C的距离:PA=________,PC=_____________
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇。
科目:初中数学 来源: 题型:
【题目】如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为![]() 小时.
小时.

(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;
(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 过点A(0,6),点D(8,0),直线
过点A(0,6),点D(8,0),直线![]() :
:![]() 与
与![]() 轴交于点C,两直线
轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)连接AC,求![]() 的面积;
的面积;
(3)若在AD上有一点P,把线段AD分成2:3的两部分时,请直接写出点P的坐标(不必写解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A.2![]() cmB.3
cmB.3![]() cmC.4
cmC.4![]() cmD.3cm
cmD.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)(2015黄石)如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.

(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王上周五在股市上以收盘价(收市时的价格)每股25元买进某公司股票1 000股,在接下来的一周交易日内,小王记下该股票每日收盘价相比前一天的涨跌情况:(单位:元)

根据上表回答问题:
(1)星期二收盘时,该股票每股______元.
(2)本周内股票收盘时的最高价______元.
(3)已知买入股票与卖出股票均需支付成交金额的千分之五的交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=![]() AD.其中正确的有( )
AD.其中正确的有( )
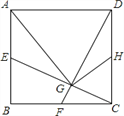
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com