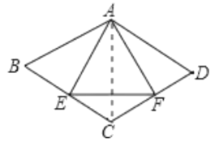
【题目】如图，菱形ABCD中，∠B=60°，AB=2cm，E、F分别是BC、CD的中点，连接AE、EF、AF，则△AEF的周长为（　　）

A.2cmB.3cmC.4cmD.3cm

参考答案：

【答案】B

【解析】

首先根据菱形的性质证明△ABE≌△ADF，然后连接AC可推出△ABC以及△ACD为等边三角形．根据等腰三角形三线合一的定理又可推出△AEF是等边三角形．根据勾股定理可求出AE的长继而求出周长．

解：连接AC，

∵四边形ABCD是菱形，
∴AB＝AD＝BC＝CD，∠B＝∠D，
∵E、F分别是BC、CD的中点，
∴BE＝DF，
在△ABE和△ADF中，
AB＝AD，∠B＝∠D，BE＝DF，

∴△ABE≌△ADF（SAS），
∴AE＝AF，∠BAE＝∠DAF．

∵∠B＝∠D＝60°，
∴△ABC与△ACD是等边三角形，
∴AE⊥BC，AF⊥CD（等腰三角形底边上的中线与底边上的高线重合），
∴∠BAE＝∠DAF＝30°，
∴∠EAF＝60°，
∴△AEF是等边三角形．
∴AE＝cm，
∴周长是3cm．
故选：B．

关闭