
【题目】如图,某公司有三个住宅区,A,B,C各区分别住有职工10人,15人,45人,且这三个区在一条大道上(A,B,C三点共线),已知AB=150m,BC=90m.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. 点A,B之间D. 点C
【答案】D
【解析】
本题为数学知识的应用,由题意设一个停靠点,分别计算所有人的路程的和再判断.
①以点A为停靠点,则所有人的路程的和=150×15+45×240=13050(米);
②以点B为停靠点,则所有人的路程的和=10×150+90×45=5550(米);
③以点C为停靠点,则所有人的路程的和=10×240+15×90=3750(米);
④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<150),则所有人的路程的和是:10m+15(150﹣m)+45(240﹣m)=13050-50m>5550 ;
⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<90),则总路程为10(150+n)+15n+45(90﹣n)=5550-20n >3750,∴该停靠点的位置应设在点C.
故选D.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)12-(-18)+(-7)-15
(2)(-2.7)+(+1![]() )-(-6.7)+(-1.6)
)-(-6.7)+(-1.6)
(3)20+(-14)-(-18)-13
(4)81÷|-2![]() |×
|×![]()
(5)![]()
(6)-14-(1-0.5×![]() )×(2-23)
)×(2-23)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为![]() 小时.
小时.

(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;
(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
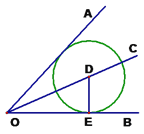
①判断⊙D与OA的位置关系, 并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A.2![]() cmB.3
cmB.3![]() cmC.4
cmC.4![]() cmD.3cm
cmD.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论:①AE+BF=![]() AB;②AE2+BF2=EF2;③S四边形CEDF=
AB;②AE2+BF2=EF2;③S四边形CEDF=![]() S△ABC;④△DEF始终为等腰直角三角形.其中正确的是( )
S△ABC;④△DEF始终为等腰直角三角形.其中正确的是( )

A.①②④B.①②③
C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com