
����Ŀ����ͼ��ʾ����ij�羰��������·��ʾ��ͼ������B��C��DΪ�羰�㣬EΪ����·�Ľ���㣬ͼ������Ϊ����Ӧ���ľ���(��λ��ǧ��)��һλ�οʹ�A����������2ǧ�ף�ʱ���ٶȲ���������ÿ������Ķ���ʱ���Ϊ![]() Сʱ��
Сʱ��

(1)��������·��A��D��C��E��A�����ص�A��ʱ��������4Сʱ����CE�ij���
(2)����ѧ�������A�������������ٶ��뾰��Ķ���ʱ�䱣�ֲ��䣬�������ʱ���ڿ����������㷵�ص�A��������Ϊ�����һ������·�ߣ�˵��������Ƶ����ɣ�
���𰸡���1��CE=0.2ǧ�ף���2������·��ӦΪA��D��C��E��B��E��A(��A��E��B��E��C��D��A)��������.
��������
��1����ϵʽΪ����·��=�ٶȡ�ʱ�䣬ע��ʱ��Ӧȥ������ʱ�䣮
��2�����ʱ���ڿ����������㷵�ص�A��Ӧѡ���ظ��߾������ڵ�·�ߣ�������Բ���CE��
��1����CE��Ϊxǧ�ף���2.2��1.4��x��1.2=2��(4��2��0.75)����ã�x=0.2��ǧ�ף���
��2��������·��ΪA��D��C��B��E��A����A��E��B��C��D��A����������ʱ��Ϊ��
��2.2��1.4��2��0.6��1.2����2��3��0.75=5.95��Сʱ����
������·��ΪA��D��C��E��B��E��A����A��E��B��E��C��D��A����������ʱ��Ϊ��
��2.2��1.4��0.2��0.6��2��1.2����2��3��0.75=5.35��Сʱ����
��Ϊ5.95��5.35�����Բ���·��ӦΪA��D��C��E��B��E��A����A��E��B��E��C��D��A����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
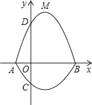
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����c1�뾭����A��D��B�������ߵ�һ����c2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0����![]() ������M��������C2��y=mx2��2mx��3m��m��0���Ķ��㣮
������M��������C2��y=mx2��2mx��3m��m��0���Ķ��㣮
��1����A��B��������ꣻ
��2�������ߡ��ڵ����������Ƿ����һ��P��ʹ�á�PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
��3������BDMΪֱ��������ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=11����BAC=120�㣬AD�ǡ�ABC�����ߣ�AE�ǡ�BAD�Ľ�ƽ���ߣ�DF��AB��AE���ӳ����ڵ�E����DF�ij�Ϊ�� ��

A. 4.5 B. 5 C. 5.5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ���˶���
���˶���![]() ����
����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ����
����![]() ��
��![]() ���߶�
���߶�![]() ��
��![]() .
.


��1����![]() ʱ��
ʱ��![]() = ��
= ��![]() = ����
= ����![]() ��
��![]() ��
��![]() �˶�ʱ��
�˶�ʱ��![]() �� ������������������С������
�� ������������������������
��2����![]() ���ڶ���ʱ��
���ڶ���ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�
��3���ڵ�![]() ���˶������У�
���˶������У�![]() ����״�����ǵ����������������ԣ���ֱ��д��
����״�����ǵ����������������ԣ���ֱ��д��![]() �Ķ���.�������ԣ���˵������.
�Ķ���.�������ԣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��˾������סլ����A��B��C�����ֱ�ס��ְ��10�ˣ�15�ˣ�45�ˣ�������������һ�������(A��B��C���㹲��)����֪AB��150m��BC��90m��Ϊ�˷���ְ�����°࣬�ù�˾�Ľ��ͳ������ڴ˼�ֻ��һ��ͣ���㣬Ϊʹ���е��˲��е�ͣ�����·��֮����С����ô��ͣ�����λ��Ӧ����(����)
![]()
A. ��AB. ��BC. ��A��B֮��D. ��C
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=a![]() ��4x+c��ͼ����A�͵�B��
��4x+c��ͼ����A�͵�B��

��1����ö��κ����ı���ʽ��
��2��д���������ߵĶԳ��ἰ�������ꣻ
��3����P��m��m�����Q���ڸú���ͼ���ϣ�����m��0��������������������ߵĶԳ���Գƣ���m��ֵ����Q��x��ľ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���鱾Уѧ����ĩƽ��ÿ������ҵ����ʱ�����������������50��ͬѧ����ͼ�Ǹ��ݵ����������ݻ��Ƶ�ͳ��ͼ��һ���֡������������Ϣ������������⣺
(1)���ÿ����ҵ��ʱ��4Сʱ������������ȫͳ��ͼ��
(2)��ε���������У�����ҵ����ʱ��������� ����λ���� ��ƽ������ ��
(3)����У����1500��ѧ��,�������ϵ��������Ƹ�Уȫ��ѧ��ÿ������ҵʱ����3Сʱ��(��3Сʱ)��ͬѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������A��B��C���㣬�ֱ��ʾ��������26����10��10������P��
A��������ÿ��1����λ���ٶ����յ�C�ƶ������P�ƶ�ʱ��Ϊt�룮

��1���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺PA=________��PC=_____________
��2������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ�����P�˶�����Cʱ��P��Q�����˶�ֹͣ��
����P��Q�����˶�ֹͣʱ�����P�͵�Q�ľ��룻
����tΪ��ֵʱP��Q����ǡ����;��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
![]()
��1��̽����
�������ϱ�ʾ7��1������֮��ľ�����_______��
�������ϱ�ʾ��2�ͩ�9������֮��ľ�����________��
��2�����ɣ�
һ��ģ������ϱ�ʾ��m����n������֮��ľ������_______��
��3��Ӧ�ã�
���������ϱ�ʾ��a�ĵ�λ�ک�5��4֮�䣬��|a+5|+|a��4|��ֵ=________��
����a��ʾ�����ϵ�һ������������|a��3|=| a+1|����a =______.
����a��ʾ�����ϵ�һ������������|a+5|+|a��4|��9����������a��ȡֵ��Χ��______.
��4����չ��
��֪����ͼA��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��10��B���Ӧ����Ϊ70.������������P��A���������3����λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�B���������2��λ/����ٶ������˶������ʱ����ֻ�������������������35����λ���ȣ���д����ʱ��P����ʾ����.
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com