
【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a,b表示,那么A、B两点之间的距离为:AB=|a-b|.利用此结论,回答以下问题:
(1)数轴上表示2和5的两点的距离是 ,数轴上表示-20和-5的两点之间的距离是 ,数轴上表示15和-30的两点之间的距离是 .
(2)数轴上表示x和-1的两点A,B之间的距离是 ,如果|AB|=2,那么x是
(3)式子|x+1|+|x-2|+|x-3|的最小值是 .
【答案】(1)3,15,45;(2)|x+1|,1或-3;(3)4.
【解析】
(1)直接根据数轴上A、B两点之间的距离|AB|=|a-b|.代入数值计算即可求任意两点间的距离;
(2)根据两点间的距离,分两种情况求解即可;
(3)根据|x-a|表示数轴上x与a之间的距离,因而原式表示:数轴上一点到-1,2和3距离的和,可知当x=2时有最小值.
解:(1)数轴上表示2和5的两点之间的距离是|2-5|=3,数轴上表示-20和-5的两点之间的距离是|-20-(-5)|=15.数轴上表示15和-30的两点之间的距离是|15-(-30)|=45;
(2)数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,如果|AB|=2,那么x+1=2或x+1=-2,∴x为1或-3;
(3)如图,当x表示的点在B点时,点B到点A、点B、点C距离之和最小,此时距离之和等于线段AB的长,
∴|x+1|+|x-2|+|x-3|表示数轴上一点到-1,2和3距离的和,最小值是4.

故答案为:(1)3,15,40;(2)|x+1|,1或-3;(3)4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)12-(-18)+(-7)-15
(2)(-2.7)+(+1![]() )-(-6.7)+(-1.6)
)-(-6.7)+(-1.6)
(3)20+(-14)-(-18)-13
(4)81÷|-2![]() |×
|×![]()
(5)![]()
(6)-14-(1-0.5×![]() )×(2-23)
)×(2-23)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
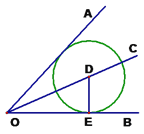
①判断⊙D与OA的位置关系, 并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应集合的括号内
+8.5, 0, -3.4, 12, -9, ![]() , 3.1415, -1.2,
, 3.1415, -1.2,![]() ,
, ![]()
(1)正数集合 { }
(2)整数集合 { }
(3)负分数集合 { }
(4)非正整数集合{ }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A.2![]() cmB.3
cmB.3![]() cmC.4
cmC.4![]() cmD.3cm
cmD.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b 与反比例函数![]() 的图象交于点A(2,m)和B(﹣6,﹣2),与y轴交于点C.
的图象交于点A(2,m)和B(﹣6,﹣2),与y轴交于点C.
(1)y1=___,y2= ;
(2)根据函数图象可知,当 y1<y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,求△ABD的面积.
(4)点P是反比例函数图象上一点,△POD的面积是5,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com