
【题目】已知抛物线![]() ,顶点为A,且经过点
,顶点为A,且经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
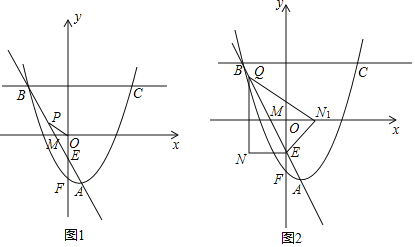
(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)(﹣
;(3)(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,2)或(
,2)或(![]() ,2).
,2).
【解析】
(1)将点B坐标代入解析式求得a的值即可;
(2)由∠OPM=∠MAF知OP∥AF,据此证△OPE∽△FAE得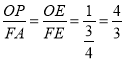 ,即OP=
,即OP=![]() FA,设点P(t,﹣2t﹣1),列出关于t的方程解之可得;
FA,设点P(t,﹣2t﹣1),列出关于t的方程解之可得;
(3)分点Q在AB上运动、点Q在BC上运动且Q在y轴左侧、点Q在BC上运动且点Q在y轴右侧这三种情况分类讨论即可得.
(1)把点![]() 代入
代入![]() ,
,
解得:a=1,
∴抛物线的解析式为:![]() ;
;
(2)由![]() 知顶点A(
知顶点A(![]() ,﹣2),
,﹣2),
设直线AB解析式为:y=kx+b,代入点A,B的坐标,
得: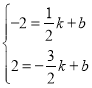 ,
,
解得:![]() ,
,
∴直线AB的解析式为:y=﹣2x﹣1,
易求E(0,﹣1),![]() ,
,![]() ,
,
∵∠OPM=∠MAF,
∴OP∥AF,
∴△OPE∽△FAE,
∴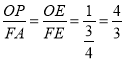 ,
,
∴![]() ,
,
设点P(t,﹣2t﹣1),则:![]()
解得![]() ,
,![]() ,
,
∵△POE的面积=![]() OE|t|,
OE|t|,
∴△POE的面积为![]() 或
或![]() .
.
(3)若点Q在AB上运动,如图1,
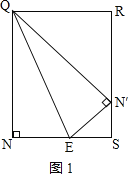
设Q(a,﹣2a﹣1),则NE=﹣a、QN=﹣2a,
由翻折知QN′=QN=﹣2a、N′E=NE=﹣a,
由∠QN′E=∠N=90°易知△QRN′∽△N′SE,
∴![]() ,即
,即![]() ,
,
∴QR=2,ES=![]() ,
,
由NE+ES=NS=QR可得﹣a+![]() =2,
=2,
解得:a=﹣![]() ,
,
∴Q(﹣![]() ,
,![]() );
);
若点Q在BC上运动,且Q在y轴左侧,如图2,
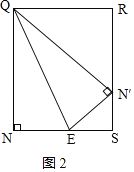
设NE=a,则N′E=a,
易知RN′=2、SN′=1、QN′=QN=3,
∴QR=![]() 、SE=
、SE=![]() ﹣a,
﹣a,
在Rt△SEN′中,(![]() ﹣a)2+12=a2,
﹣a)2+12=a2,
解得:a=![]() ,
,
∴Q(﹣![]() ,2);
,2);
若点Q在BC上运动,且点Q在y轴右侧,如图3,
设NE=a,则N′E=a,
易知RN′=2,SN′=1,QN′=QN=3,
∴QR=![]() ,SE=
,SE=![]() ﹣a,
﹣a,
在Rt△SEN′中,(![]() ﹣a)2+12=a2,
﹣a)2+12=a2,
解得:a=![]() ,
,
∴Q(![]() ,2).
,2).
综上,点Q的坐标为(﹣![]() ,
,![]() ))或(﹣
))或(﹣![]() ,2)或(
,2)或(![]() ,2).
,2).


科目:初中数学 来源: 题型:
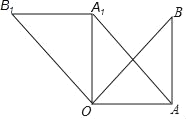
【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB,将△OAB物点O逆时针方向旋转90°得到△OA1B1.
(1)求∠AOB1的度数;
(2)连结AA1,求证:四边形OAA1B1是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
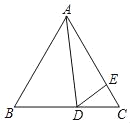
【题目】如图,等边△ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°
(1)求证:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐火车从上海到娄底,高铁G1329次列车比快车K575次列车少需要9小时,已知上海到娄底的铁路长约1260千米,G1329的平均速度是K575的2.5倍.
(1)求K575的平均速度;
(2)高铁G1329从上海到娄底只需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
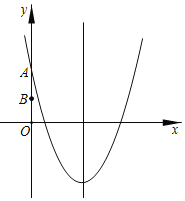
【题目】如图,抛物线y=![]() ﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.
﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
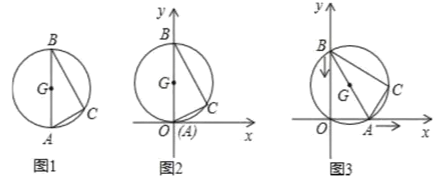
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2,现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束,在整个运动过程中,点C运动的路径长是( )
A.![]() πB.2πC.4
πB.2πC.4![]() -2D.10-4
-2D.10-4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(Ⅰ)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(Ⅱ)试探究直线![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(Ⅲ)已知点![]() ,且
,且![]() ,
,![]() 在抛物线
在抛物线![]()
![]() 上,若当
上,若当![]() (其中
(其中![]() )时,函数
)时,函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
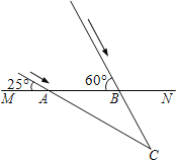
【题目】 两支探险队进行探险活动,如图,甲队沿与公路MN夹角为25°方向前进,乙队沿与公路MN夹角为60°方向前进,分别经过公路MN于A、B两点,且AB距离为10km,两支探险队相遇于点C,则点C距公路MN的距离是多少?(结果精确到1km.参考数据sin25°≈0.40,cos25°≈0.90,tan25°≈0.50,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com