
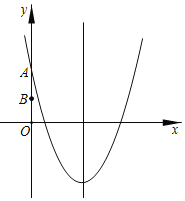
【题目】如图,抛物线y=![]() ﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.
﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.
【答案】10.
【解析】
作点A关于抛物线y=![]() ﹣4x+4的对称轴的对称点A',作点B关于x轴的对称点B',连接A'B',分别交x轴、抛物线对称轴于点M、N,则BM+MN+NA就是点G运动的最短路径,由对称的性质得AN=A'N,BM=B'M,得出点G运动的最短路径=BM+MN+NA=A'B',求出抛物线y=
﹣4x+4的对称轴的对称点A',作点B关于x轴的对称点B',连接A'B',分别交x轴、抛物线对称轴于点M、N,则BM+MN+NA就是点G运动的最短路径,由对称的性质得AN=A'N,BM=B'M,得出点G运动的最短路径=BM+MN+NA=A'B',求出抛物线y=![]() ﹣4x+4的对称轴为直线x=4,点A的坐标为(0,4),A'的坐标为(8,4),B的坐标为(0,2),B'的坐标为(0,﹣2),得出AB'=6,AA'=8,由勾股定理求出A'B'=
﹣4x+4的对称轴为直线x=4,点A的坐标为(0,4),A'的坐标为(8,4),B的坐标为(0,2),B'的坐标为(0,﹣2),得出AB'=6,AA'=8,由勾股定理求出A'B'=![]() =10即可.
=10即可.
解:作点A关于抛物线y=![]() ﹣4x+4的对称轴的对称点A',作点B关于x轴的对称点B',连接A'B',分别交x轴、抛物线对称轴于点M、N,如图所示:
﹣4x+4的对称轴的对称点A',作点B关于x轴的对称点B',连接A'B',分别交x轴、抛物线对称轴于点M、N,如图所示:
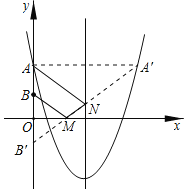
则BM+MN+NA就是点G运动的最短路径,由对称的性质得:AN=A'N,BM=B'M,
∴点G运动的最短路径=BM+MN+NA=A'B',
∵抛物线y=![]() ﹣4x+4=
﹣4x+4=![]() (x﹣4)2﹣4,
(x﹣4)2﹣4,
∴抛物线y=![]() ﹣4x+4的对称轴为直线x=4,
﹣4x+4的对称轴为直线x=4,
当x=0时,y=4,即点A的坐标为(0,4),
∴点A'的坐标为(8,4),
∵B是OA的中点,
∴B的坐标为(0,2),
∴B'的坐标为(0,﹣2),
∴AB'=4+2=6,AA'=8,
∴A'B'=![]() =
=![]() =10,
=10,
即点G走过的最短路程为10;
故答案为:10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
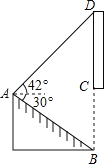
【题目】2021年世界园艺博览会将在扬州枣林湾举办,有一块枣林湾博览会的直传牌CD竖立在路边,其中CB是支柱.小梅同学想计算出CD的长度.于是在A处测得支柱B处的俯角为30°.测得顶端D处的仰角为42°,同时测量出AB的长度是10m,BC的长度是6m.求宜传牌CD的长度(结果保留小数点后一位).(参考数据:![]() ≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,顶点为A,且经过点
,顶点为A,且经过点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
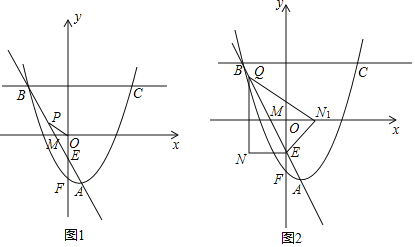
(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为(1,4)的抛物线![]() 与直线
与直线![]() 交于点A(2,2),直线
交于点A(2,2),直线![]() 与
与![]() 轴交于点B与
轴交于点B与![]() 轴交于点C
轴交于点C
(1)求![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
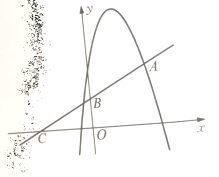
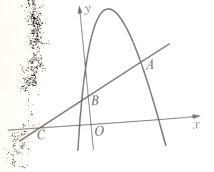
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.25人中至少有3人的出生月份相同
B.任意抛掷一枚均匀的1元硬币,若上一次正面朝上,则下一次一定反面朝上
C.天气预报说明天降雨的概率为10%,则明天一定是晴天
D.任意抛掷一枚均匀的骰子,掷出的点数小于3的概率是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com