
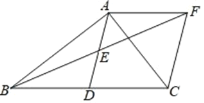
【题目】在△ABC 中,∠BAC=90°,AD 是 BC 边上的中线,点 E 为 AD 的中点,过点 A 作 AF∥BC交 BE 的延长线于点 F,连接 CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形 ADCF 为正方形;
②连接 DF,当∠ACB= °时,四边形 ABDF 为菱形.
【答案】(1)见解析;(2)①45;②30
【解析】
(1)根据直角三角形的性质得到AD=CD=BD,根据全等三角形的判定和性质即可得到结论;
(2)①根据菱形的判定定理得到四边形ADCF是菱形,求得∠DCF=90°,于是得到结论;
②根据平行四边形的性质得到CD=CF,推出△DCF是等边三角形,得到DF=BD,于是得到结论.
(1)∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)①当∠ACB=45°时,四边形ADCF为正方形;
∵AD=AF,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是菱形,
要使四边形ADCF是正方形,
则∠DCF=90°,
∴∠ACD=∠ACF=45°;
②当∠ACB=30°时,四边形ABDF为菱形;
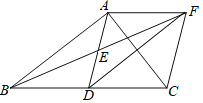
由(1)得AF=BD,AF∥BC,
∴四边形ABDF是平行四边形,
要使四边形ABDF为菱形,
∴AB=BD,
又∵AD =BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ACB=30°.
故答案为:45,30.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC
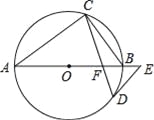
(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
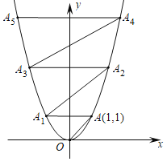
【题目】在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象是直线
的图象是直线![]() ,点A(14,1)是
,点A(14,1)是![]() 与反比例函数y=
与反比例函数y=![]() 的图象的交点.
的图象的交点.
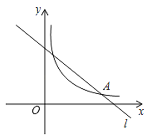
(1)一次函数与反比例函数的表达式;
(2)将直线![]() 平移后得直线
平移后得直线![]() ,与y轴正半轴交于点B(0,t),同时交
,与y轴正半轴交于点B(0,t),同时交![]() 轴于点C,若S△ABC=18,求t的值.
轴于点C,若S△ABC=18,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点P(2,6),过点P作PA⊥x轴于A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,若tan∠DCO=2.
的图象交于点P(2,6),过点P作PA⊥x轴于A,PB⊥y轴于点B.一次函数的图象分别交x轴、y轴于点C、D,若tan∠DCO=2.
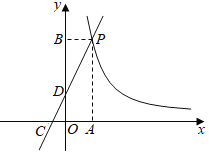
(1)求一次函数与反比例函数的解析式;
(2)求△BDP的面积,并根据图象写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com