
【题目】在平面直角坐标系中,抛物线y=x2的图象如图所示.已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2019的坐标为_______.
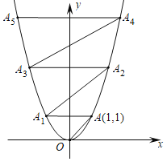
【答案】(-1010,10102)
【解析】
根据二次函数性质可得出点A1的坐标,求得直线A1A2为y=x+2,联立方程求得A2的坐标,即可求得A3的坐标,同理求得A4的坐标,即可求得A5的坐标,根据坐标的变化找出变化规律,即可找出点A2019的坐标.
∵A点坐标为(1,1),
∴直线OA为y=x,A1(-1,1),
∵A1A2∥OA,
∴直线A1A2为y=x+2,
解![]() 得
得![]() 或
或![]() ,
,
∴A2(2,4),
∴A3(-2,4),
∵A3A4∥OA,
∴直线A3A4为y=x+6,
解![]() 得
得![]() 或
或![]() ,
,
∴A4(3,9),
∴A5(-3,9)
…,
∴A2019(-1010,10102),
故答案为(-1010,10102).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
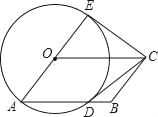
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD、CE,若CE是⊙O的切线.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,OC=7,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
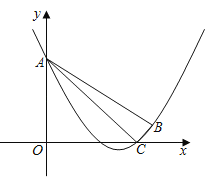
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BM是以AB为直径的⊙O的切线,B为切点,BC平分∠ABM,弦CD交AB于点E,DE=OE.

(1)求证:△ACB是等腰直角三角形;
(2)求证:OA2=OEDC:
(3)求tan∠ACD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:

(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价![]() (元/件)之间存在一次函数关系,求y关于
(元/件)之间存在一次函数关系,求y关于![]() 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
(3)为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
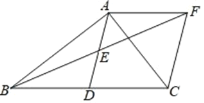
【题目】在△ABC 中,∠BAC=90°,AD 是 BC 边上的中线,点 E 为 AD 的中点,过点 A 作 AF∥BC交 BE 的延长线于点 F,连接 CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形 ADCF 为正方形;
②连接 DF,当∠ACB= °时,四边形 ABDF 为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
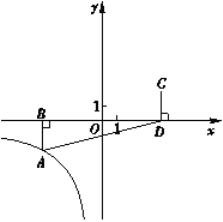
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com