
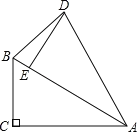
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,将△ABC绕点A顺时针旋转得△ADE,点C的对应点E恰好落在AB上.
(1)求∠DBC的度数;
(2)当BD![]() 时,求AD的长.
时,求AD的长.
【答案】(1)135°;(2)AD![]() 1.
1.
【解析】
(1)根据旋转的性质得到三角形ABD为等腰三角形,利用等腰三角形的性质求出∠ABD即可解决问题;
(2)设AD=AB=2x,则DE=![]() AD=x,AE=
AD=x,AE=![]() x,利用勾股定理构建方程即可解决问题.
x,利用勾股定理构建方程即可解决问题.
(1)∵∠C=90°,∠ABC=60°,
∴∠BAC=∠DAB=30°.
根据旋转的性质得:AD=AB,
∴∠ABD=∠ADB![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠DBC=∠ABD+∠ABC=75°+60°=135°;
(2)设AD=AB=2x,则DE![]() AD=x,AE
AD=x,AE![]() x,
x,
∴BE=2x![]() x,
x,
在Rt△BDE中,
∵BD2=DE2+BE2,
∴2=x2+(2x![]() x)2,
x)2,
解得:x![]() ,
,
∴AD=2x![]() 1.
1.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
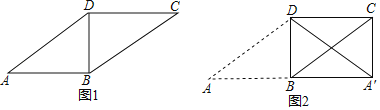
【题目】如图1,在平行四边形ABCD中,对角线BD⊥AB,以BD为对称轴将△ABD翻折,点A的对应点为A′,连接A′C,得到图2.
推理证明
(1)求证:四边形A′BDC是矩形;
实践操作
(2)在图1中将△ABD或△BDC进行平移、旋转或轴对称变换,重新构造一个特殊四边形.
要求:①画出图形,标明字母;②写出构图过程及构造的特殊四边形的名称.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,

回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,4)、B(﹣4,0)、C(0,﹣4)、D(4,0),对于图形M,给出如下定义:点P为图形M上任意一点,点Q为正方形ABCD边上任意一点,如果P、Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).
(1)已知点E(0,2),G(﹣1,﹣1).
①如图1,直接写出d(点E),d(点G)的值;
②如图2,扇形EOF圆心角∠EOF=45°,将扇形EOF绕点O顺时针旋转α角(0<α<180°)得到扇形E'OF',当d(扇形E'OF')取最大值时,求α角的取值范围;
(2)点P为平面内一动点,且满足d(点P)=6,直接写出OP长度的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线段AE为边作正方形AEFG,连接EB,GD.
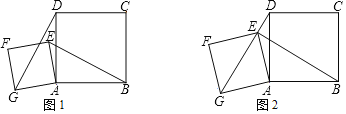
(1)如图1,求证EB=GD;
(2)如图2,若点E在线段DG上,AB=5,AG=3![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D为第四象限抛物线上一点,设点D的横坐标为m,四边形ABCD的面积为S,求S与m的函数关系式,并求S的最值;
(3)点P在抛物线的对称轴上,且∠BPC=45°,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com