

分析 不同,分别以A、B、C为坐标原点建立坐标系,求出其它两点的坐标,用待定系数法求解析式即可.
解答 解:要求该抛物线的函数表达式,你认为首先要做的工作是:确定坐标原点建立坐标系;
分别以A、B、C为坐标原点建立坐标系,所得函数表达式不同;
(1)以A为原点建立坐标系,则A(0,0),B(12,0),C(6,4)
设y=a(x-h)2+k,
∵C为顶点,
∴y=a(x-6)2+4,
把A(0,0)代入上式,
36a+4=0,
解得:a=-$\frac{1}{9}$,
∴y=-$\frac{1}{9}$(x-6)2+4;
(2)以B为坐标原点建立坐标系,则A(-12,0),B(0,0)C(-6,4)
设y=a(x-h)2+k,
∵C为顶点,
∴y=a(x+6)2+4,
把B(0,0)代入上式,
36a+4=0,
解得:a=-$\frac{1}{9}$,
∴y=-$\frac{1}{9}$(x+6)2+4;
(3)以C为坐标原点建立坐标系,则A(-6,-4),B(6,-4)C(0,0)
设y=ax2,
把B(6,-4)代入上式,
36a+4=0,
解得:a=-$\frac{1}{9}$,
∴y=-$\frac{1}{9}$x2;
所以方法(3)取法求得的函数表达式最简单.
点评 本题主要考查了待定系数法求二次函数解析式,恰当的选取坐标原点,求出各点的坐标是解决问题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | 总体是10万个纪念章,样本是500个纪念章 | |
| B. | 总体是10万个纪念章,样本是498个纪念章 | |
| C. | 总体是500万个纪念章,样本是500个纪念章 | |
| D. | 总体是10万个纪念章,样本是2个纪念章 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )
如图,在边长为1的正方形构成的网络中,半径为1的⊙O的圆心在格点上,则图中阴影部分两个小扇形的面积之和为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
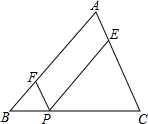 如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.
如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
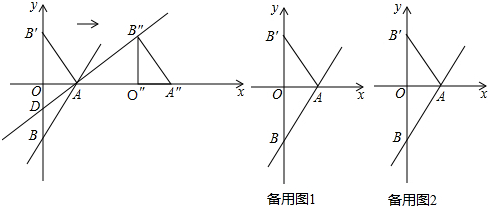
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com