
如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长
线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.

(1)证明见解析;(2)PG=PB+DG,证明见解析;(3)存在.3;理由见解析.
【解析】
试题分析::(1)过点F作FH⊥BE于点H,利用正方形的性质,证得△BAP≌△HPF得出PH=AB,BP=FH进一步得出BP+PC=PC+CH,CH=BP=FH,∠FHC=90°,求得∠DCF=90°-45°=45°得出结论;
(2)延长PB至K,使BK=DG,连接AK,证得△ABK≌△ADG和△KAP≌△GAP,找出边相等得出结论;
(3)首先判定存在,在直线AB上取一点M,使四边形DMPF是平行四边形,证得△ABP≌△DAM,进一步球的结论即可.
(1)证明:过点F作FH⊥BE于点H,

∵四边形ABCD是正方形,
∴∠ABC=∠PHF=∠DCB=90º,AB=BC,
∴∠BAP+∠APB=90º
∵AP⊥PF,
∴∠APB+∠FPH=90º
∴∠FPH=∠BAP
又∵AP=PF
∴△BAP≌△HPF
∴PH=AB,BP=FH
∴PH=BC
∴BP+PC=PC+CH
∴CH=BP=FH
而∠FHC=90º. ∴∠FCH=CFH=45º
∴∠DCF=90º-45º=45º
∴∠GCF=∠FCE
(2)PG=PB+DG
证明:延长PB至K,使BK=DG,
∵四边形ABCD是正方形
∴AB=AD, ∠ABK=ADG=90º
∴△ABK≌△ADG
∴AK=AG, ∠KAB=∠GAD,
而∠APF=90 º,AP=PF
∴∠PAF=∠PFA=45 º
∴∠BAP+∠KAB=∠KAP=45 º=∠PAF
∴△KAP≌△GAP
∴KP=PG,
∴KB+BP=DG+BP=PG
即,PG=PB+DG
(3)存在.
如图,在直线AB上取一点M,使四边形DMPF是平行四边形,
则MD∥PF,且MD=FP,
又∵PF=AP,
∴MD=AP
∵四边形ABCD是正方形 ,
∴AB=AD,∠ABP=∠DAM
∴△ABP≌△DAM
∴AM=BP=2,
∴BM=AB-AM=5-2=3.
∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形.
考点:1.正方形的性质;2.全等三角形的判定与性质;3.平行四边形的判定.


科目:初中数学 来源:2013-2014学年湖北省黄冈市中考模拟考试数学试卷A(解析版) 题型:解答题
如图,已知直线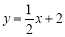 与坐标轴相交于A、B两点,与双曲线
与坐标轴相交于A、B两点,与双曲线 交于点C.A、D两点关于y轴对称若四边形OBCD的面积为6,求k的值.
交于点C.A、D两点关于y轴对称若四边形OBCD的面积为6,求k的值.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省黄冈市九年级下学期入学考试数学试卷(解析版) 题型:选择题
如果将一组数据中的每个数据都加上同一个非零常数,那么这组数据的 ( )
A.平均数和方差都不变 B.平均数不变,方差改变
C.平均数改变,方差不变 D.平均数和方差都改变
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省鄂州市九年级4月调研考试数学试卷(解析版) 题型:选择题
在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省襄阳市襄州区九年级中考适应性测试数学试卷(解析版) 题型:解答题
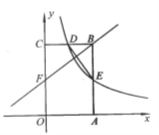
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点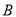 的坐标为(2,3).双曲线
的坐标为(2,3).双曲线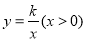 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且ΔFCB∽ΔDBE,求直线FB的解析式
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
已知关于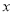 的方程
的方程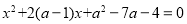 .
.
(1)若方程有两个不相等的实数根,求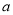 的取值范围;
的取值范围;
(2)若方程的两个实数根为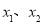 ,且满足
,且满足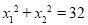 ,求
,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:选择题
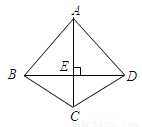
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
A.AB=AD B.AC平分∠BCD C.AB=BD D.△BEC≌△DEC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com