
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() .
.
【解析】试题分析: ![]() 把点
把点![]() 的坐标代入即可求得抛物线的解析式.
的坐标代入即可求得抛物线的解析式.
![]() 作BH⊥AC于点H,求出
作BH⊥AC于点H,求出![]() 的长度,即可求出∠ACB的度数.
的长度,即可求出∠ACB的度数.
![]() 延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线
延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线![]() 的方程,和抛物线的方程联立即可求得点
的方程,和抛物线的方程联立即可求得点![]() 的坐标.
的坐标.
试题解析:(1)由题意,得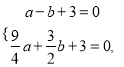
解得![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(![]() ,0),
,0),
∴AC=![]() ,AB=
,AB=![]() ,OC=3,BC=
,OC=3,BC=![]() .
.
∵![]() ,即∠BAD=
,即∠BAD= ![]() ,
,
∴![]() .
.
Rt△ BCH中, ![]() ,BC=
,BC=![]() ,∠BHC=90,
,∠BHC=90,
∴![]() .
.
又∵∠ACB是锐角,∴![]() .
.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=![]() ,
,
∴![]() .
.
∵△DCE∽△AOC,∴只可能∠CAO=∠DCE.
∴AG = CG.
∴ .
.
∴AG=5.∴G点坐标是(4,0).
∵点C坐标是(0,3),∴![]() .
.
∴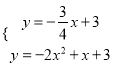 解得
解得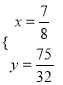 ,
, ![]() (舍).
(舍).
∴点D坐标是![]()


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(0,10),点B(m,10)在第一象限,连接AB、OB.
(1)如图1,若OB=12,求m的值.

(2)如图2,当m=10时,过B作BC⊥x轴于C,E为AB边上一点,AE=![]() ,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.
,把△OAE沿直线OE翻折得到△OFE(点A的对应点为点F),连接BF、CF,求证:BF⊥CF.

(3)如图3,将△AOB沿直线OB翻折得到△GOB(点A的对应点为点G),若点G到x轴的距离不大于8,直接写出m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;

图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.

图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题:
例题:若![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]() ,求
,求![]() 和
和![]() 的值.
的值.
解:![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]()
![]() +
+![]() +
+![]() +
+![]() -
-![]() +
+![]() =
=![]()
![]() (
(![]() )
)![]() +(
+(![]() -
-![]() )
)![]() =
=![]()
![]() -
-![]() =
=![]()
![]() -
-![]() ,
,![]()
问题:(1)若![]() -
-![]() -
-![]() =
=![]() , 求
, 求![]() 的值;
的值;
(2)已知![]() 的三边长
的三边长![]() 都是正整数,且满足
都是正整数,且满足![]() -
-![]() -
-![]() +
+![]() │3-
│3-![]() │=
│=![]() ,请问
,请问![]() 是怎样形状的三角形.
是怎样形状的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级有350名师生需要租车去野外进行拓展训练,现有A、B两种类型号的车可供选择,已知1辆A型车和2辆B型车可载110人,2辆A型车和1辆B型车可载100人。
(1)A、B型车每辆可分别载多少人?
(2)要始每辆车都恰好坐满且正好运完这些师生,请问你有哪几种设计租车方案,请一一列举出来。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市教育局决定分别配发给一中8台电脑,二中10台电脑,但现在仅有12台,需
在商场购买6台. 从市教育局运一台电脑到一中、二中的运费分别是30元和50元,从商场
运一台电脑到一中、二中的运费分别是40元和80元. 要求总运费不超过840元,问有几
种调运方案?指出运费最低的方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABC中∠A=60°,AB=2cm,AC=6cm,点P、Q分别是边AB、AC上的动点,点P从顶点A沿AB以1cm/s的速度向点B运动,同时点Q从顶点C沿CA以3cm/s的速度向点A运动,当点P到达点B时点P、Q都停止运动.设运动的时间为t秒.

(1)当t为何值时AP=AQ;
(2)是否存在某一时刻使得△APQ是直角三角形,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
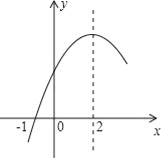
其中正确结论的序号是_______________.(在横线上填上你认为所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com