
����Ŀ����ͼ1����ƽ��ֱ������ϵx0y�У�ֱ��![]() ��y�ύ�ڵ�A����x�ύ�ڵ�B��������
��y�ύ�ڵ�A����x�ύ�ڵ�B��������![]() ��
��![]() ��A��B���㣬��x�����һ����Ϊ��C.
��A��B���㣬��x�����һ����Ϊ��C.

��1����������![]() �Ľ���ʽ����C�����ꣻ
�Ľ���ʽ����C�����ꣻ
��2����ͼ2����������![]() ��ʹ��������
��ʹ��������![]() ��
��![]() ǡ�ù���ԭ��Գƣ�
ǡ�ù���ԭ��Գƣ�![]() ��
��![]() �ڵ�һ�����ڽ��ڵ�D������AD��CD.
�ڵ�һ�����ڽ��ڵ�D������AD��CD.
����ֱ��д��������![]() �Ľ���ʽ�͵�D�����ꣻ
�Ľ���ʽ�͵�D�����ꣻ
�����ı���AOCD�������
��3����֪������![]() ���Ķ���ΪM����PΪ������
���Ķ���ΪM����PΪ������![]() �Գ�����һ�㣬QΪֱ��
�Գ�����һ�㣬QΪֱ��![]() ��һ�㣬�Ƿ�����Ե�M��Q��P��BΪ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵������.
��һ�㣬�Ƿ�����Ե�M��Q��P��BΪ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵������.
���𰸡���1��������C1�Ľ���ʽΪ��y=-![]() x2+
x2+![]() x+4��C��8��0����
x+4��C��8��0����
��2����������C2�Ľ���ʽΪy=![]() x2+
x2+![]() x-4��D��4��6������S�ı���AOCD=32��
x-4��D��4��6������S�ı���AOCD=32��
��3�������Ե�M��Q��P��BΪ������ı���Ϊƽ���ı��Σ���P������ΪP��3��![]() ����P��3��
����P��3��![]() ����
����
��������
��1�������ֱ��y=2x+4��x�ᡢy�ύ�����꣬����ϵ�����������߽���ʽ���ɣ�
��2���ٸ����������߹���ԭ��Գƣ���������C1�Ľ���ʽ�е�x��y�ֱ�-x��-y��������Ϊ������C2�Ľ���ʽ����ͨ���ⷽ�������D�����ꣻ
�����ı���AOCD�����������D��DE��x����E�����ı���AOCD�ָ��һ�����κ�һ��ֱ�������μ�����ã�
��3����B��BN��y�ᣬ��M��MN��x����BN���ڵ�N�����������ηֱ����P�����꣺��BMΪƽ���ı��εıߣ���BMΪƽ���ı��εĶԽ��ߣ�
��1����ֱ��y=2x+4��y�ύ�ڵ�A����x�ύ�ڵ�B��
��A��0��4����B��-2��0����
��������C1��![]() ��A��B���㣬
��A��B���㣬
��c=4��0=-![]() ����-2��2-2b+4�����b=
����-2��2-2b+4�����b=![]() ��
��
��������C1�Ľ���ʽΪ��y=-![]() x2+
x2+![]() x+4��
x+4��
��y=0����-![]() x2+
x2+![]() x+4=0�����x1=-2��x2=8��
x+4=0�����x1=-2��x2=8��
��C��8��0����
��2���١�������C2��C1ǡ�ù���ԭ��Գƣ�
��������C2�Ľ���ʽΪy=![]() x2+
x2+![]() x-4��
x-4��
�ⷽ���� ��
��
�ã� ��
�� ��
��
�ߵ�D�ڵ�һ�����ڣ���D��4��6����
����ͼ��
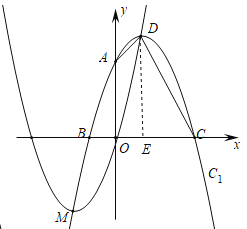
��D��DE��x����E����OE=4��CE=OC-OE=8-4=4��DE=6��
S�ı���AOCD=S����AOED+S��CDE=![]() ��OA+DE����OE+
��OA+DE����OE+![]() DE��CE=
DE��CE=![]() ��4+6����4+
��4+6����4+![]() ��6��4=32��
��6��4=32��
��3�����ڣ�
��ͼ��
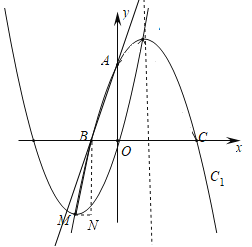
��B��BN��y�ᣬ��M��MN��x����BN���ڵ�N��
��������C2�Ľ���ʽΪy=![]() x2+
x2+![]() x-4=
x-4=![]() (x+3)2-
(x+3)2-![]() ��
��
�ඥ��M��-3��-![]() ����
����
��BN=![]() ��MN=1��
��MN=1��
������C1�ĶԳ���Ϊ��ֱ��x=3����P��3��m����
���Ե�M��Q��P��BΪ������ı���Ϊƽ���ı��Σ���MQΪ�Խ��ߣ���BM��PQ��BM=PQ��
��Q��4��m+![]() ����
����
�֡�QΪֱ��y=2x+4��һ�㣬
��m+![]() =2��4+4����ã�m=
=2��4+4����ã�m=![]() ��
��
��P��3��![]() ����
����
����BMΪ�Խ��ߣ���P��3��m����Q��n��2n+4����
��BM�е�����Ϊ��-![]() ��/span>
��/span>![]() ����
����
�� �����
����� ��
��
��P��3��![]() ����
����
����BQΪ�Խ��ߣ���BM��PQ��BM=PQ��
��Q��2��8������P��3��m����
��m-![]() =8+0����ã�m=
=8+0����ã�m=![]() ��
��
��P��3��![]() ����
����
���������������Ե�M��Q��P��BΪ������ı���Ϊƽ���ı��Σ���P������ΪP��3��![]() ����P��3��
����P��3��![]() ����
����


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
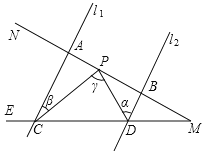
����Ŀ����ͼ����֪l1��l2������MN�ֱ��ֱ��l1��l2����A��B������ME�ֱ��ֱ��l1��l2����C��D����P��A��B���˶���P��A��B���㲻�غϣ������PDB=������PCA=������CPD=����
��1����̽������������֮���к�������ϵ��˵�����ɣ�
��2�����BD=3��AB=9��AC=6������AC��ֱ��MN����ô��P�˶���ʲôλ��ʱ����ACP�ա�BPD˵�����ɣ�
��3���ڣ�2���������£�����ACP�ա�BPDʱ��PC��PD֮���к�λ�ù�ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ�������
����λ���ȵ��ٶ�������![]() �����˶�������
�����˶�������![]() ��
��![]() ��������
��������![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() Ϊ�ڱ���
Ϊ�ڱ���![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() .
.
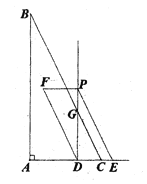
��1���߶�![]() �ij�Ϊ ���ú�
�ij�Ϊ ���ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2�����![]() ����
����![]() ��ʱ
��ʱ![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]()
![]() ���ص�����ͼ�ε����Ϊ
���ص�����ͼ�ε����Ϊ![]() ��ƽ����λ������
��ƽ����λ������![]() ʱ����
ʱ����![]() ��
��![]() ֮��ĺ�����ϵʽ.
֮��ĺ�����ϵʽ.
��4����![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() Ϊ����������ʱ
Ϊ����������ʱ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ��Խ���AC��BD�ཻ�ڵ�O��DH��AB�ڵ�H������OH����CAD��20�������DHO�Ķ����ǣ�������
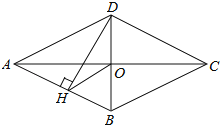
A.20��B.25��C.30��D.40��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��x2��5x��6��x���Ϸ���ͼ����x�ᷭ�۵�x���·���ͼ������ಿ�ֲ��䣬�õ�һ����ͼ����ֱ��y��2x+b�������ͼ����3�������㣬��b��ֵΪ��������
A. ��![]() ��12B. ��
��12B. ��![]() ��2C. ��12��2D. ��
��2C. ��12��2D. ��![]() ��12
��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ѧϰ�����ľ��飬�Ժ���y=x+![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=x+![]() ���Ա���x��ȡֵ��Χ��_____��
���Ա���x��ȡֵ��Χ��_____��
��2���±��г���y��x�ļ����Ӧֵ����д��m��n��ֵ��m=_____��n=_____��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | 4 | �� |
y | �� | �� | �� | ��2 | �� | �� | m |
| 2 |
| n |
| �� |
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ����
��4����Ϻ�����ͼ������ɣ�
�ٵ�y=��![]() ʱ��x=_____��
ʱ��x=_____��
��д���ú�����һ������_____��
��������x+![]() =t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
=t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
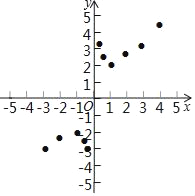
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
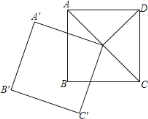
����Ŀ����ͼ��������ABCD�����Ϊ8cm2������Խ����ཻ�ڵ�O����O��������A��B��C��O��һ�����㣬������������εı߳���ȣ���ô������A��B��C��O�Ƶ�O��������ת���������������ص����ֵ����Ϊ_____cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�![]() �У�
��![]() ��
��![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() .
.

��1����֤��![]() ��
��
��2��ij��ѧ��ȤС����1�����֣���ͼ��ֻ�轫![]() ������ƴ��
������ƴ��![]() �����Ϳɵõ�һ����
�����Ϳɵõ�һ����![]() ������ľ���
������ľ���![]() �������ۺ��ַ��֣�����������Ҳ���Լ�ƴ��һ��������ľ��Σ�������ͼ���л���һ�ּ�ƴʾ��ͼ������Ҫ˵������������Ҫ֤����
�������ۺ��ַ��֣�����������Ҳ���Լ�ƴ��һ��������ľ��Σ�������ͼ���л���һ�ּ�ƴʾ��ͼ������Ҫ˵������������Ҫ֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
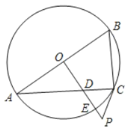
����Ŀ����ͼ����֪![]() ��
��![]() ��ֱ������
��ֱ������![]() ����
����![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����ʹ
����ʹ![]() .
.
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com