
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向运动,过点
方向运动,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作
为邻边作![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
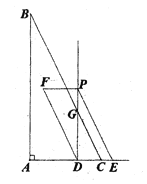
(1)线段![]() 的长为 (用含
的长为 (用含![]() 的代数式表示)
的代数式表示)
(2)求点![]() 落在
落在![]() 上时
上时![]() 的值;
的值;
(3)设![]() 与
与![]()
![]() 的重叠部分图形的面积为
的重叠部分图形的面积为![]() (平方单位),当
(平方单位),当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当![]() 时,直接写出
时,直接写出![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图 1,已知抛物线 y ax![]() bx c 经过 A3,0,B 1,0 ,C 0,3 三点,其顶点为D,对称轴是直线l , l 与 x 轴交于点 H .
bx c 经过 A3,0,B 1,0 ,C 0,3 三点,其顶点为D,对称轴是直线l , l 与 x 轴交于点 H .
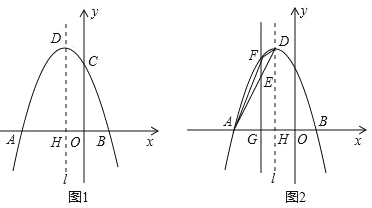
(1)求该抛物线的解析式;
(2)若点 P 是该抛物线对称轴l 上的一个动点,求PBC 周长的最小值;
(3)如图 2,若 E 是线段 AD 上的一个动点( E 与 A, D 不重合),过 E 点作平行于 y 轴的直线交抛物线于点 F ,交 x 轴于点G ,设点 E 的横坐标为m ,四边形 AODF 的面积为 S 。
①求 S 与 m 的函数关系式;
② S 是否存在最大值,若存在,求出最大值及此时点 E 的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,通过记录,发现该商品从开始销售至销售的第x天结束时(x为整数)的总销量y(件)满足二次函数关系,销量情况记录如下表:
x | 0 | 1 | 2 | 3 |
y | 0 | 58 | 112 | 162 |
(1)求y与x之间的函数关系式(不需要写自变量的取值范围);
(2)求:销售到第几天结束时,该商品全部售完?
(3)若第m天的销量为22件,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,且销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
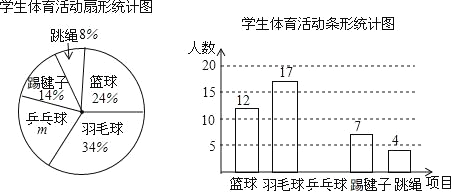
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
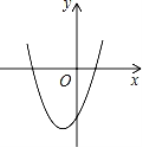
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该商品每天的销售利润最大;
(3)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系x0y中,直线![]() 与y轴交于点A,与x轴交于点B,抛物线
与y轴交于点A,与x轴交于点B,抛物线![]() :
:![]() 过A、B两点,与x轴的另一交点为点C.
过A、B两点,与x轴的另一交点为点C.

(1)求抛物线![]() 的解析式及点C的坐标;
的解析式及点C的坐标;
(2)如图2,作抛物线![]() ,使得抛物线
,使得抛物线![]() 与
与![]() 恰好关于原点对称,
恰好关于原点对称,![]() 与
与![]() 在第一象限内交于点D,连接AD,CD.
在第一象限内交于点D,连接AD,CD.
①请直接写出抛物线![]() 的解析式和点D的坐标;
的解析式和点D的坐标;
②求四边形AOCD的面积;
(3)已知抛物线![]() ,的顶点为M,设P为抛物线
,的顶点为M,设P为抛物线![]() 对称轴上一点,Q为直线
对称轴上一点,Q为直线![]() 上一点,是否存在以点M,Q,P,B为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
上一点,是否存在以点M,Q,P,B为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(k+1)x+![]() k2+1=0
k2+1=0
(1) 当k取何值方程有两个实数根
(2) 是否存在k值使方程的两根为一个矩形的两邻边长,且矩形的对角线长为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com