练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一元二次方程x2﹣4x+4=0的根的情况是（ ）
    A.有两个不相等的实数根
    B.有两个相等的实数根
    C.无实数根
    D.无法确定

    【答案】B
    【解析】解：在方程x2﹣4x+4=0中， △=（﹣4）2﹣4×1×4=0，
    ∴该方程有两个相等的实数根．
    故选B．
    将方程的系数代入根的判别式中，得出△=0，由此即可得知该方程有两个相等的实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，小明做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是( )

    A. SAS B. ASA C. AAS D. SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市一月份的营业额为300万元，已知三月份的营业额为363万元，如果平均每月的增长率为x，由题意列方程________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查发现，截至2016年底某市汽车拥有量为16.9万辆，已知2014年底该市汽车拥有量为10万辆，设2014年底至2016年底该市汽车拥有量的年平均增长率为x，根据题意可列方程得（ ）
    A.10（1﹣x）2=16.9
    B.10（1+2x）=16.9
    C.10（1+x）2=16.9
    D.16.9（1+x）2=10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将下列各数填在相应的大括号里：

    1， —5， ， —4.2， 0， , 10，—，

    整数：｛ … ｝

    非负整数：｛ … ｝

    分数：｛ … ｝

    负分数：｛ … ｝

    有理数：｛ … ｝

    非负有理数：｛ … ｝

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三角形的三条中位线的长度分别为6cm、7cm、11cm，则三角形的周长为cm.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

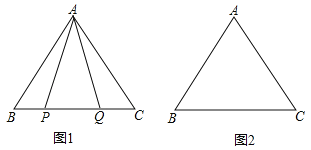
    【题目】在等边△ABC中：

    （1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；

    （2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．

    ①依题意将图2补全；

    ②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：要证明PA=PM，只需证△APM是等边三角形；

    想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；

    想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…

    请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a+b=5，ab=-6，则代数式ab2+a2b的值是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用代数式表示.

    (1)“x的5倍与y的和的一半”可以表示为_____.

    (2)南平乡有水稻田m亩，计划每亩施肥a千克；有玉米田n亩，计划每亩施肥b千克，共施肥_____千克.

    (3)有三个连续的整数，最小数是m，则其他两个数分别是_____和_____.

    (4)全班总人数为y，其中男生占56%，那么女生人数是_____.

    查看答案和解析>>

    同步练习册答案