
【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.
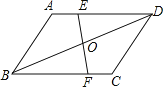
【答案】(1)详见解析;(2)四边形EBFD是菱形
【解析】
(1)连接BE、DF,证明四边形EBFD为平行四边形,根据平行四边形的性质即可求解.
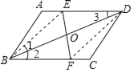
(2)根据BD平分∠EBF,可得∠1=∠2,由平行线的性质可得∠3=∠2,等量代换可得∠1=∠3,即可证明BE=ED,即可判定四边形EBFD的形状.
解:(1)证明:连接BE、DF,
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴OE=OF;
(2)解:四边形EBFD是菱形.理由如下:
∵BD平分∠EBF,
∴∠1=∠2,
∵AD∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴BE=ED,
∴平行四边形EBFD是菱形.


科目:初中数学 来源: 题型:
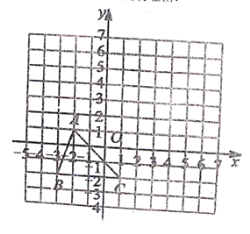
【题目】已知:如图把![]() 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到![]() .
.
(1)在图中画出![]() ;
;
(2)写出点![]() 的坐标:
的坐标:![]() 的坐标为______,
的坐标为______,![]() 的坐标为 _________;
的坐标为 _________; ![]() 的坐标为________.
的坐标为________.
(3)在![]() 轴上是否存在一点P,使得
轴上是否存在一点P,使得![]() 的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.
的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任选一题作答,只计一题的成绩:
a.如图,在![]() 的正方形网格中,点
的正方形网格中,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上.连接点
都在格点上.连接点![]() ,
,![]() 得线段
得线段![]() .
.

(1)画出过![]() ,
,![]() ,
,![]() ,
,![]() 中的任意两点的直线;
中的任意两点的直线;
(2)互相平行的直线(线段)有 ;(请用“![]() ”表示)
”表示)
(3)互相垂直的直线(线段)有 .
(请用“![]() ”表示)
”表示)
b.如图,直线![]() 和
和![]() 相交于
相交于![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的度数.
的度数.
其中一种解题过程如下,请在括号中注明根据,在横线上补全步骤.
解:![]()
![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的角平分线
的角平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.
(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈ ![]() ,sin31°≈
,sin31°≈ ![]() ,tan39°≈
,tan39°≈ ![]() ,sin39°≈
,sin39°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用13000元购进甲、乙两种矿泉水共400箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价/(元·箱 | 销售价/(元·箱 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这400箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上,老师组织同学们以“探索等腰三角形的边长与周长的关系”为主题展开数学活动.请你解决活动过程中产生的问题.
操作发现:已知![]() 是等腰三角形.如果它的两条边长分别为
是等腰三角形.如果它的两条边长分别为![]() 和
和![]() 求它的周长.小明的做法是分为腰长为
求它的周长.小明的做法是分为腰长为![]() 和
和![]() 两种情况,进行计算.
两种情况,进行计算.
![]() 请你帮助小明补上计算过程;
请你帮助小明补上计算过程;
继续探索:如果它的两条边长分别为![]() 和
和![]() 求它的周长;
求它的周长;
![]() 此时它的周长还是两种结果吗?请说明理由,并求出此时等腰三角形的周长;
此时它的周长还是两种结果吗?请说明理由,并求出此时等腰三角形的周长;
活学活用:
![]() 如果它的周长为
如果它的周长为![]() 一条边长为
一条边长为![]() 则它的腰长为 .
则它的腰长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,按如下顺序依次排列为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 根据这个规律,第
根据这个规律,第![]() 个点的坐标为( )
个点的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(﹣4,0)
(1)求点D的坐标;
(2)设点P是边BC上(不与点B、C重合)的一个动点,设点P的坐标为(m,0),△ABP的面积为S,求△ABP的面积S关于m的函数关系式,并写出自变量m的取值范围;
(3)直接写出当△ABP为等腰三角形时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com