
����Ŀ����ѡһ������ֻ��һ��ijɼ���
a.��ͼ����![]() �������������У���
����������������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ڸ���ϣ����ӵ�
���ڸ���ϣ����ӵ�![]() ��
��![]() ���߶�
���߶�![]() ��
��

��1��������![]() ��
��![]() ��
��![]() ��
��![]() �е����������ֱ�ߣ�
�е����������ֱ�ߣ�
��2������ƽ�е�ֱ�ߣ��߶Σ����� �������á�![]() ����ʾ��
����ʾ��
��3�����ഹֱ��ֱ�ߣ��߶Σ����� ����
��������![]() ����ʾ��
����ʾ��
b.��ͼ��ֱ��![]() ��
��![]() �ཻ��
�ཻ��![]() ��
��![]() ��
��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ����
����![]() �Ķ�����
�Ķ�����
����һ�ֽ���������£�����������ע�����ݣ��ں����ϲ�ȫ���裮
�⣺![]()
![]()
![]() ����
���� ![]()
![]() �� ��
�� ��![]()
![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����
![]() �� ��
�� ��![]()
![]() �� ��
�� ��![]()
![]() �� ��
�� ��![]()
![]() �� ��
�� ��![]()
![]()
![]() �� ��
�� ��![]()
![]() �� ��
�� ��![]()
![]() �� ��
�� ��![]()

���𰸡�a.��1�������������2��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ��
��![]() ��
��
b.��֪��![]() ��
��![]() ����ƽ���߶��壻
����ƽ���߶��壻![]() ��
��![]() ��ƽ�Ƕ��壻
��ƽ�Ƕ��壻![]() ��ͬ�ǵ�������
��ͬ�ǵ�������
��������
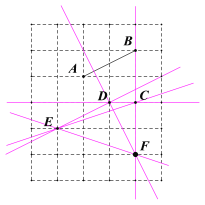
a.��1������ֱ�ߵĶ����![]() ��
��![]() ��
��![]() ��
��![]() �е����������ֱ�߿�������6��ֱ�ߣ���2������ƽ���ߵ��ж����ɵó��𰸣���3�����ݴ��ߵĶ��弴�ɵó��𰸣�
�е����������ֱ�߿�������6��ֱ�ߣ���2������ƽ���ߵ��ж����ɵó��𰸣���3�����ݴ��ߵĶ��弴�ɵó��𰸣�
b.���ݻ���ǵĶ��塢��ƽ���ߵĶ��塢ƽ�ǵĶ��塢ͬ�ǵ�����������⼴�ɣ�
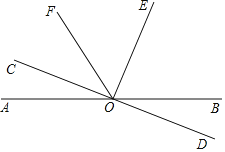
a���⣺��1����ͼ��
��2��![]() ��
��![]() ��
��
��3��![]() ��
��![]() ��
��![]() ��
��
b.�⣺ ![]()
![]()
![]() ������֪
������֪ ![]()
��![]() ��
��
![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����
��![]() ����ƽ���߶���
����ƽ���߶���
��![]() ��
��
��![]() ��
��
![]()
![]() ��ƽ�Ƕ��� ��
��ƽ�Ƕ��� ��![]()
��![]() ��ͬ�ǵ���������
��ͬ�ǵ���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����ABCD�Ķ���A������Ϊ��2��0������B������Ϊ��0��1�����Խ���BD��x��ƽ�У���ֱ��y��kx+5+2k��k��0��������ABCD�н��㣬��k��ȡֵ��Χ�ǣ�������
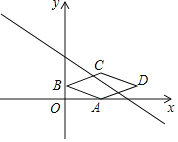
A.![]() B.
B.![]()
C.![]() D.��2��k��2��k��0
D.��2��k��2��k��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=5��AB=4����E��F��ֱ��AD�ϣ����ı���BCFEΪ���Σ����߶�EF���е�Ϊ��M�����߶�AM�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������C1��y=ax2+bx+4��x�ύ��A����3��0����B���㣬��y�ύ�ڵ�C����M���� ![]() ��5����������C1��һ�㣬������C2��������C1����y��Գƣ���A��B��M����y��ĶԳƵ�ֱ�Ϊ��A�䡢B�䡢M�䣮
��5����������C1��һ�㣬������C2��������C1����y��Գƣ���A��B��M����y��ĶԳƵ�ֱ�Ϊ��A�䡢B�䡢M�䣮
��1����������C1�Ľ���ʽ��
��2������M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A�䡢D��PΪ��������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ��ij������9��00������������ԱС��������칫�ҳ���������Ϊ����������������Ա��ͥ��������Ʒ��ͬʱ�˽������Ա�Ľ���״��������ȥ�˾��������Ͻ����żң�����ͣ����ѯ�����������ȥ����Զһ�����ң�����˿ڽ϶࣬�˽����ʱ���Գ�һЩ����������������������ȴ����������������������ٷ��������칫�ң���֪С����������칫�ҵľ���![]() ���ף����뿪�칫�ҵ�ʱ��
���ף����뿪�칫�ҵ�ʱ��![]() ���֣�֮��Ĺ�ϵ��ͼ��ʾ�������ͼ��ش��������⣺
���֣�֮��Ĺ�ϵ��ͼ��ʾ�������ͼ��ش��������⣺

��1��ͼ��![]() ���ʾ��������ʲô��
���ʾ��������ʲô��
��2��С�����ҳ������е��ٶ��Ƕ��٣�
��3��С�������ͣ���˼����ӣ�С�X��ص������칫�ң�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ� ��A������Ϊ��2��4��.
��1��������ABC����x��ԳƵġ�A1B1C1����д����A�Ķ�Ӧ������A1 ��
��2��������A1B1C1��ԭ��O��ת180���õ��ġ�A2B2C2����д����A2������A2 ��
��3����BC���ϵĸ�AD����AD= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
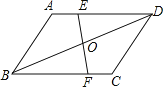
����Ŀ����֪����ͼ����ABCD�У���E��F�ֱ���AD��BC�ϣ�EF��BD�ཻ�ڵ�O��AE=CF��
��1����֤��OE=OF��
��2������BE��DF����BDƽ�֡�EBF�����ж��ı���EBFD����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʪ�أ�ˮ���γǡ���ijУ��ѧ��ȤС��͡�����ȥ���γ������ξ��㡱��������˱�У����ѧ����Ҫ��ÿλͬѧѡ����ֻ��ѡ��һ������ȥ�ľ��㣬�����Ǹ��ݵ���������������������Ƴ��IJ�������ͳ��ͼ��

�����ͼ���ṩ����Ϣ������������⣺
��1�������ѧ����������
��2����ȫ����ͳ��ͼ����������ͳ��ͼ�б�ʾ������ȥ����D��������Բ�ĽǵĶ�����
��3������У����800��ѧ��������ơ�����ȥ����B����ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�EF���Խ��ߵĽ���O�������AB��CD�ֱ��ཻ�ڵ�E��F��AB��5��AD��3��OF��1.5�����ı���BCFE���ܳ�Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com