
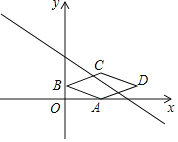
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),对角线BD与x轴平行,若直线y=kx+5+2k(k≠0)与菱形ABCD有交点,则k的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.﹣2≤k≤2且k≠0
D.﹣2≤k≤2且k≠0
【答案】B
【解析】
依据直线y=kx+5+2k即可得到直线y=kx+5+2k(k≠0)经过定点P(-2,5),再根据直线PD的解析式为![]() ,直线PB的解析式为y=-2x+1,直线y=kx+5+2k(k≠0)与菱形ABCD有交点,即可得到k的取值范围.
,直线PB的解析式为y=-2x+1,直线y=kx+5+2k(k≠0)与菱形ABCD有交点,即可得到k的取值范围.
如图,
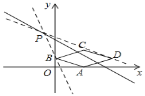
在直线y=kx+5+2k(k≠0)中,令x=﹣2,则y=5,
∴直线y=kx+5+2k(k≠0)经过定点P(﹣2,5),
由菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),
可得C(2,2),D(4,1),
∴易得直线PD的解析式为![]() ,直线PB的解析式为y=﹣2x+1,
,直线PB的解析式为y=﹣2x+1,
∵直线y=kx+5+2k(k≠0)与菱形ABCD有交点,
∴k的取值范围是![]() ,
,
故选B.


科目:初中数学 来源: 题型:
【题目】在“绿满重庆”行动中,江北区种植了大量的小叶榕和银杏树,根据林业专家的分析,树叶在进行光合作用后产生的分泌物能在空气中吸附悬浮颗粒,这样就达到了滞尘净化空气的作用.
(1)若某小区今年要种植银杏树和小叶榕共450株,且银杏树的数量不超过小叶榕数量的2倍,求今年该小区小叶榕至少种植多少株?
(2)已知每一片银杏树叶一年平均滞尘量为![]() ,一株银杏树去年有3500片树叶,冬季树叶全部掉落后,今年新长出了树叶,且这株银杏今年的滞尘量是去年滞尘量的1.1倍还多
,一株银杏树去年有3500片树叶,冬季树叶全部掉落后,今年新长出了树叶,且这株银杏今年的滞尘量是去年滞尘量的1.1倍还多![]() .已知每片小叶榕树叶的滞尘量比银杏树叶多
.已知每片小叶榕树叶的滞尘量比银杏树叶多![]() ,一株小叶榕今年的树叶总量比今年的这株银杏要少
,一株小叶榕今年的树叶总量比今年的这株银杏要少![]() ,明年这株小叶榕树叶将在今年的基础上掉落
,明年这株小叶榕树叶将在今年的基础上掉落![]() ,但又会新长出1000片树叶,若今明两年这株小叶榕共滞尘量为
,但又会新长出1000片树叶,若今明两年这株小叶榕共滞尘量为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到矩形AnBnCnDn(n>2).

(1)求AB1和AB2的长.
(2)若ABn的长为56,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,ABCD中,E,F分别是AB、CD上的点,AE=CF,M、N分别是DE、BF的中点.
(1)求证:四边形ENFM是平行四边形.
(2)若∠ABC=2∠A,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°,∠A=30°
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作△ABC的外接圆O;
②在AB的延长线上作一点D,使得CD与⊙O相切;
(2)综合与运用:在你所作的图中,若AC=6,则由线段CD,BD及 ![]() 所围成图形的面积为 .
所围成图形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿矩形的边由![]() 运动,设点P运动的路程为x,
运动,设点P运动的路程为x,![]() 的面积为y,把y看作x的函数,函数的图像如图2所示,则
的面积为y,把y看作x的函数,函数的图像如图2所示,则![]() 的面积为( )
的面积为( )

A. 10 B. 16 C. 18 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任选一题作答,只计一题的成绩:
a.如图,在![]() 的正方形网格中,点
的正方形网格中,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上.连接点
都在格点上.连接点![]() ,
,![]() 得线段
得线段![]() .
.

(1)画出过![]() ,
,![]() ,
,![]() ,
,![]() 中的任意两点的直线;
中的任意两点的直线;
(2)互相平行的直线(线段)有 ;(请用“![]() ”表示)
”表示)
(3)互相垂直的直线(线段)有 .
(请用“![]() ”表示)
”表示)
b.如图,直线![]() 和
和![]() 相交于
相交于![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的度数.
的度数.
其中一种解题过程如下,请在括号中注明根据,在横线上补全步骤.
解:![]()
![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的角平分线
的角平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com