
【题目】如图,四边形ABCD是平行四边形,AB=5,BC=10,顶点A在y轴上,边BC在x轴上,且点B的坐标为(﹣4,0)
(1)求点D的坐标;
(2)设点P是边BC上(不与点B、C重合)的一个动点,设点P的坐标为(m,0),△ABP的面积为S,求△ABP的面积S关于m的函数关系式,并写出自变量m的取值范围;
(3)直接写出当△ABP为等腰三角形时点P的坐标.

【答案】(1)点D的坐标为(10,3);(2)![]() (
(![]() );(3)点P的坐标为(4,0)或(1,0)或(﹣
);(3)点P的坐标为(4,0)或(1,0)或(﹣![]() ,0).
,0).
【解析】
(1)根据勾股定理求出OA,根据平行四边形的性质求出点D的坐标;
(2)分点P在OB上和点P在OC上两种情况,根据三角形的面积公式计算即可;
(3)分AB=AP、AB=BP、AP=BP三种情况,根据等腰三角形的性质、勾股定理解答.
(1)∵点B的坐标为(﹣4,0)
∴OB=4,
∴OA=![]() ,
,
∵AD=BC=10,
∴点D的坐标为(10,3);
(2)![]() (
(![]() ),
),
则![]() 关于m的函数关系式为:
关于m的函数关系式为:![]() (
(![]() );
);

(3)当AB=AP时,OP=OB=4,
则点P的坐标为(4,0),
当AB=BP=5时,OP=BP﹣OB=1,
则点P的坐标为(1,0),
如图,当AP=BP时,BP=AP=OB﹣OP=4﹣OP,
由勾股定理得,OP2+OA2=AP2,即(4﹣OP)2=32+OP2,
解得,OP=![]() ,
,
则点P的坐标为(﹣![]() ,0),
,0),
综上所述,当△ABP为等腰三角形时点P的坐标为(4,0)或(1,0)或(﹣![]() ,0).
,0).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
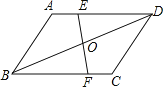
【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=﹣1是对称轴,有下列判断:
①b﹣2a=0;②4a﹣2b+c<0;③a﹣b+c=﹣9a;④若(﹣3,y1),( ![]() ,y2)是抛物线上两点,则y1>y2 , 其中正确的是( )
,y2)是抛物线上两点,则y1>y2 , 其中正确的是( )
A.①②③
B.①③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F,AB=5,AD=3,OF=1.5,则四边形BCFE的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】声音在空气中传播的速度![]() (简称音速)与气温
(简称音速)与气温![]() 的关系如下表:
的关系如下表:
气温 | 0 | 5 | 10 | 15 | 20 |
音速 | 331 | 334 | 337 | 340 | 343 |
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速![]() 与气温
与气温![]() 之间的关系式.
之间的关系式.
(3)气温![]()
![]() 时,某人看到烟花燃放
时,某人看到烟花燃放![]() 后才听到声音,那么此人与燃放烟花的所在地约相距多远?
后才听到声音,那么此人与燃放烟花的所在地约相距多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由![]() ,因为
,因为![]() ,请确定
,请确定![]() 是______位数;
是______位数;
(2)由32768的个位上的数是8,请确定![]() 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为![]() ,请确定
,请确定![]() 的十位上的数是_____________;
的十位上的数是_____________;
(3)已知![]() 和
和![]() 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算:![]() ;
;![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,A、B分别为直线
,A、B分别为直线![]() 、
、![]() 上两点,且
上两点,且![]() ,若射线
,若射线![]() 绕点顺时针旋转至
绕点顺时针旋转至![]() 后立即回转,射线
后立即回转,射线![]() 绕点B逆时针旋转至
绕点B逆时针旋转至![]() 后立即回转,两射线分别绕点A、点B不停地旋转,若射线
后立即回转,两射线分别绕点A、点B不停地旋转,若射线![]() 转动的速度是
转动的速度是![]() /秒,射线
/秒,射线![]() 转动的速度是
转动的速度是![]() /秒,且a、b满足
/秒,且a、b满足![]() .若射线
.若射线![]() 绕点A顺时针先转动18秒,射线
绕点A顺时针先转动18秒,射线![]() 才开始绕点B逆时针旋转,在射线
才开始绕点B逆时针旋转,在射线![]() 到达
到达![]() 之前,问射线
之前,问射线![]() 再转动_______秒时,射线
再转动_______秒时,射线![]() 与射线
与射线![]() 互相平行.
互相平行.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com