
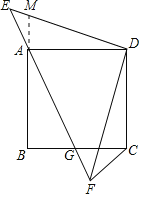
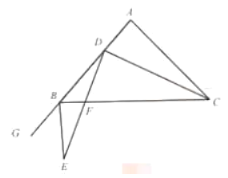
【题目】如图,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.

(1)求证:△DAE≌△DCF;
(2)求证:△ABG∽△CFG;
(3)若正方形ABCD的的边长为2,G为BC的中点,求EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3) EF=![]() .
.
【解析】
(1)根据正方形的性质有AD=CD,根据等腰直角三角形的性质有DE=DF,已知两边尝试找其夹角对应相等,根据等角的余角相等可得,∠ADE=∠CDF,据此可证;
(2)此题有多种方法可解,可以延长BA交DE与M,结合第(1)问全等三角形的结论用等角做差求得∠BAG=∠FCG,再加上一对对顶角相等即可证明;
(3)根据第(2)问相似三角形的结论,易得![]() ,在Rt△CFG中得到了两直角边CF与FG的倍数关系,再运用勾股定理即可解出CF与FG的长度,又AE=CF,即可解答.
,在Rt△CFG中得到了两直角边CF与FG的倍数关系,再运用勾股定理即可解出CF与FG的长度,又AE=CF,即可解答.
证明:(1)∵正方形ABCD,等腰直角三角形EDF,
∴∠ADC=∠EDF=90°,AD=CD,DE=DF,
∴∠ADE+∠ADF=∠ADF+∠CDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
![]() ,∠
,∠![]() =∠
=∠![]() ,
,![]() ;
;
∴△ADE≌△CDF(SAS);
(2)延长BA到M,交ED于点M,
∵△ADE≌△CDF,
∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,
∵∠MAD=∠BCD=90°,
∴∠EAM=∠BCF,
∵∠EAM=∠BAG,
∴∠BAG=∠BCF,
∵∠AGB=∠CGF,
∴△ABG∽△CFG.
(3)∵正方形ABCD的的边长为2,G为BC的中点,
∴BG=CG=1,
AG=![]() ,
,
∵△ABG∽△CFG,
∴![]() ,
,
CF=2FG,
∵CF2+FG2=CG2,
(2FG)2+FG2=12,
∴GF=![]() ,CF=
,CF=![]() ,
,
∵△DAE≌△DCF,
∴AE=CF,
∴EF=EA+AG+GF=CF+AG+GF=![]() +
+![]() +
+![]() =
=![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】“一带一路”为我们打开了交流、合作的大门,也为沿线各国在商贸等领域提供了更多的便捷,2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举办,据哈外贸商会发布消息,博览会期间,哈Paseka公司与重庆某国际贸易公司签订了供应蜂蜜合同:哈Paseka公司于2019年6月前分期分批向重庆某国际贸易公司供给优质蜂蜜共3000万件,该公司顺应新时代购物流,打算分线上和线下两种方式销售.
(1)若计划线上销售量不低于线下销售量的25%,求该公司计划在线下销售量最多为多少万件?
(2)该公司在12月上旬销售优质蜂蜜共240万件,且线上线下销售单件均为100元/件.12月中旬决定线上销售单价下调m%,线下销售单价不变,在这种情况下,12月中旬销售总量比上旬增加了m%,且中旬线上销售量占中旬总销量的![]() ,结果中旬销售总金额比上旬销售总金额提高了
,结果中旬销售总金额比上旬销售总金额提高了![]() m%.求m的值.
m%.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
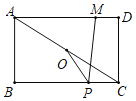
【题目】如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
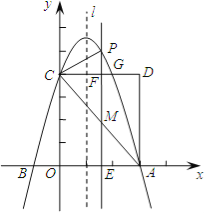
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件60元的价格购进一批货物,零售价为每件80元时,可以卖出100件(按相关规定零售价不能超过80元).如果零售价在80元的基础上每降价1元,可以多卖出10件,当零售价在80元的基础上降价x元时,能获得2160元的利润,根据题意,可列方程为( )
A.x(100+10x)=2160B.(20﹣x)(100+10x)=2160
C.(20+x)(100+10x)=2160D.(20﹣x)(100﹣10x)=2160
查看答案和解析>>
科目:初中数学 来源: 题型:
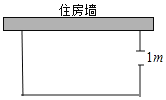
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点(点
上的动点(点![]() 不与点
不与点![]() 重合),点
重合),点![]() 在边
在边![]() 的延长线上,
的延长线上,![]() ,
,![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)点![]() 在边
在边![]() 上运动的过程中,
上运动的过程中,![]() 的值是否会发生变化?如果不变化,请求
的值是否会发生变化?如果不变化,请求![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转60°,得到△AED,点B、C的对应点分别是E、D.F为AC的中点,连接BF、DF、BE,DF与EA相交于点G,BE与AC相交于点H.
(1)如图1,求证:四边形BFDE为平行四边形;
(2)如图2,连接CE,在不添加任何辅助线与字母的情况下,请直接写出所有与△AEC全等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
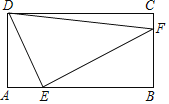
【题目】如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF,已知AB=4cm,AD=2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了x与y的几组值,如表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
(说明:补全表格时相关数值保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(4)结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com